GPTDAOCN-e/acc on Nostr: 揭开贝叶斯定理的神秘面纱：概率推理的视觉盛宴！ ...

揭开贝叶斯定理的神秘面纱：概率推理的视觉盛宴！

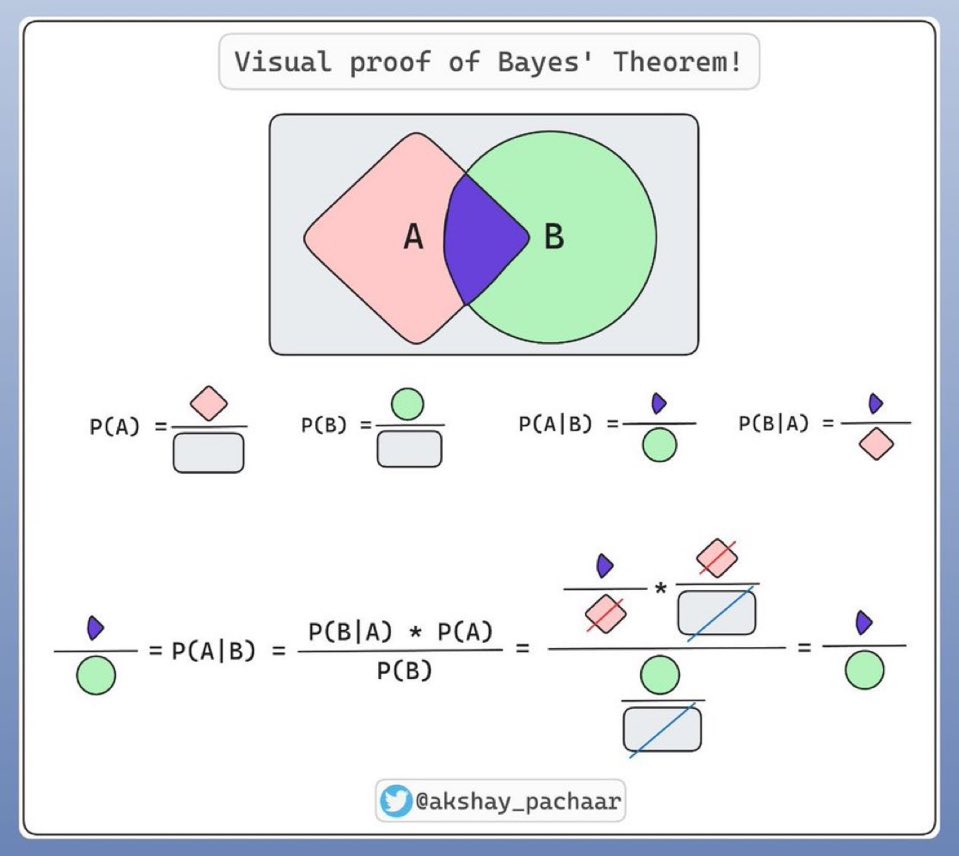
这幅图是贝叶斯定理的可视化证明，帮助理解事件概率之间的关系。

1. 区域表示：
- A和B：分别是两个事件，用不同颜色表示。
- 重叠部分：表示A和B同时发生的概率，即联合概率。

2. 概率符号：
- P(A)：事件A发生的概率。
- P(B)：事件B发生的概率。
- P(A|B)：在B已发生的条件下，A发生的概率（条件概率）。
- P(B|A)：在A已发生的条件下，B发生的概率。

3. 贝叶斯定理公式：
\[
P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}
\]
- 用于计算在已知B发生的情况下，A发生的概率。
- 通过计算，展示了如何利用已知信息更新对某事件发生概率的判断。

直观理解：

- 条件概率：图中用形状和颜色区分不同事件及其组合，帮助理解如何从一个事件的信息推导出另一个事件的信息。
- 乘法与除法关系：展示了如何通过乘积和比率关系来计算复杂概率。

这个可视化图解有助于更直观地理解贝叶斯定理在统计推断中的应用。