nick on Nostr: 🧭🪄 FROST: a treasure hunt 🏴☠️📜 You can think of FROST like clues ...
🧭🪄 FROST: a treasure hunt 🏴☠️📜
You can think of FROST like clues of a treasure map.
You need a certain number of clues (threshold) to piece together where the treasure lies.
Each secret share (clue) is a point on a polynomial (overall treasure map), where the y-intercept is the joint secret (location of the treasure) that no single party knows.
Every party in the multisig controls their own clue,
With secret shares at indexes like:
Party1: (1, s_1)
Party2: (2, s_2)
...
A threshold number of parties can take their clues to interpolate the polynomial and find the treasure.
Or better yet, what if they could use their clues to spend the treasure without recombining the full treasure map!
FROST allows this, where parties can do computation using their clues to access the treasure without any party ever knowing exactly where the treasure is.
e.g. sign a message using the joint secret.
To enroll a new party into the multisig, we need to create a new clue for our treasure map. A threshold number of parties can work together to create a new clue that makes sense with the existing treasure map, and securely communicate it to the new participant
A new point on this polynomial: (n, S_n)
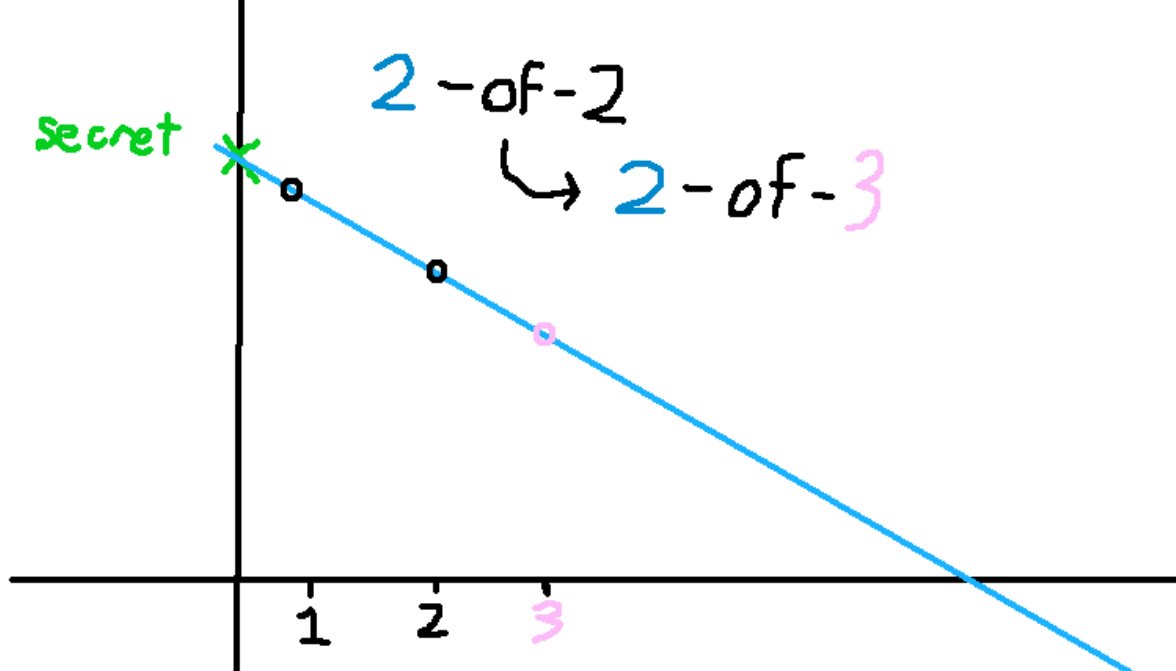
You can even communicate a new clue to someone without them knowing that it helps lead them to treasure. This is the premise of my ideas for private collaborative custodians. Someone can hold a secret share without them learning of the public key.
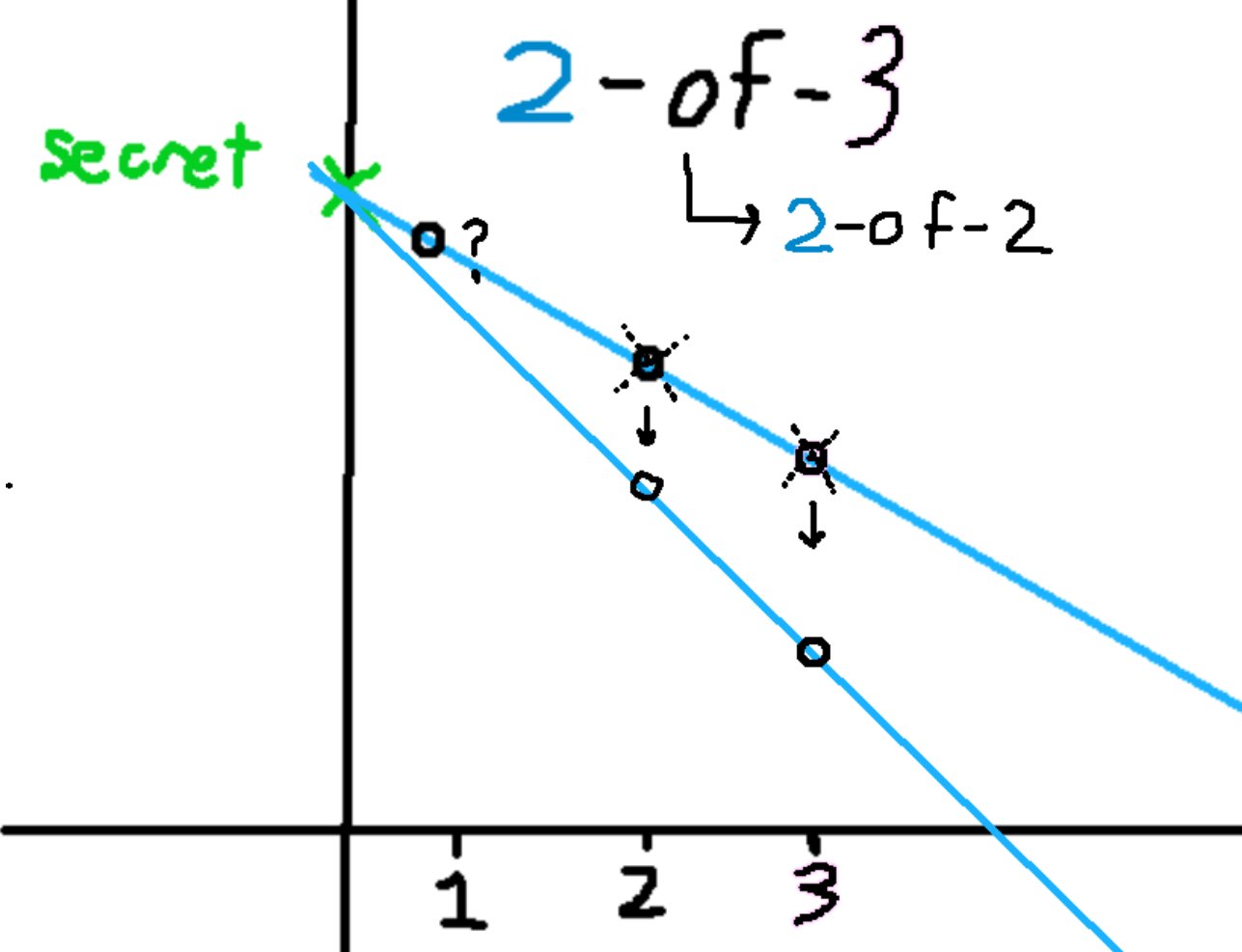
To remove a party from the multisig, a threshold number of parties work together to create a new treasure map that leads to the same treasure, and update their clues so that they make no sense when used with clues from the old treasure map.
In FROST terms, Parties can update their secret shares to lie on a new polynomial that interpolates the same joint secret. They delete their old secret shares.
In this extremely scientific diagram, Parties 2 and 3 update their shares, and delete the old ones.
Party 1's share is now incompatible and is effectively removed.
---
Thinking this treasure map analogy is useful, what do you think?
(also, im not using windows i just rate ms paint)
You can think of FROST like clues of a treasure map.
You need a certain number of clues (threshold) to piece together where the treasure lies.
Each secret share (clue) is a point on a polynomial (overall treasure map), where the y-intercept is the joint secret (location of the treasure) that no single party knows.
Every party in the multisig controls their own clue,
With secret shares at indexes like:
Party1: (1, s_1)
Party2: (2, s_2)
...
A threshold number of parties can take their clues to interpolate the polynomial and find the treasure.
Or better yet, what if they could use their clues to spend the treasure without recombining the full treasure map!
FROST allows this, where parties can do computation using their clues to access the treasure without any party ever knowing exactly where the treasure is.
e.g. sign a message using the joint secret.
To enroll a new party into the multisig, we need to create a new clue for our treasure map. A threshold number of parties can work together to create a new clue that makes sense with the existing treasure map, and securely communicate it to the new participant
A new point on this polynomial: (n, S_n)

You can even communicate a new clue to someone without them knowing that it helps lead them to treasure. This is the premise of my ideas for private collaborative custodians. Someone can hold a secret share without them learning of the public key.
To remove a party from the multisig, a threshold number of parties work together to create a new treasure map that leads to the same treasure, and update their clues so that they make no sense when used with clues from the old treasure map.
In FROST terms, Parties can update their secret shares to lie on a new polynomial that interpolates the same joint secret. They delete their old secret shares.
In this extremely scientific diagram, Parties 2 and 3 update their shares, and delete the old ones.
Party 1's share is now incompatible and is effectively removed.

---
Thinking this treasure map analogy is useful, what do you think?
(also, im not using windows i just rate ms paint)
