keychat on Nostr: Over the past few weeks, we have been learning and testing the MLS protocol and have ...
Over the past few weeks, we have been learning and testing the MLS protocol and have gained a deeper understanding of it. Below is a note providing a general description of the MLS protocol.
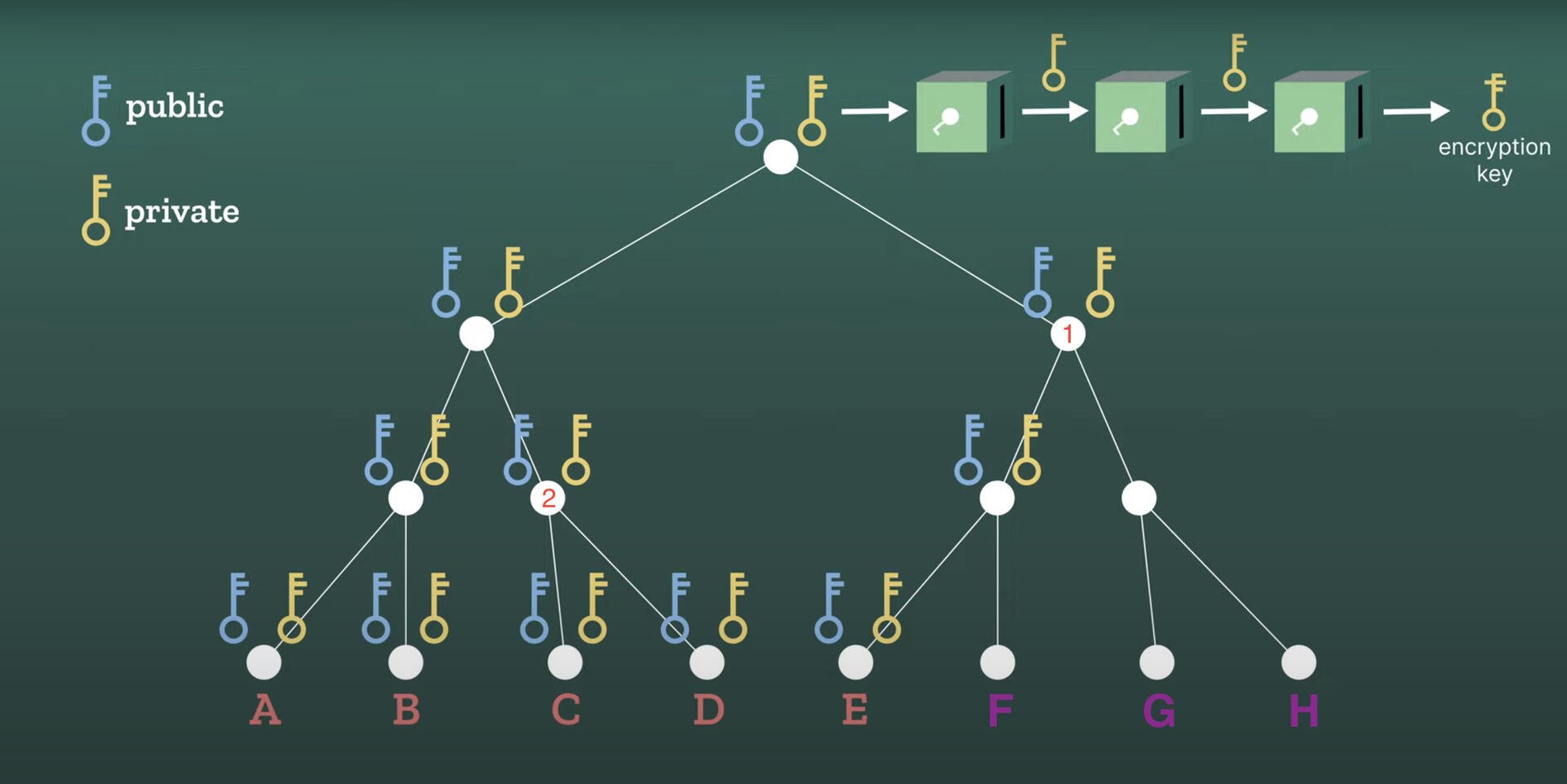
The MLS group members (A, B, C, D, E, F, G, H) form the leaf nodes of a binary tree as shown below. Each member has a pair of public and private keys.
For member A, they use their private key  and member B’s public key  to perform an ECDH computation. For member B, they use their private key  and member A’s public key  to perform an ECDH computation.
Both compute the same value. This value becomes the private key of Node3, and from this, the public key of Node3 can also be derived.
Similarly, other members perform their respective ECDH computations.
Moreover, nodes higher in the tree also perform their respective ECDH computations up to the Root. Node3 and Node4 compute the private key of Node1 through ECDH, while Node5 and Node6 compute the private key of Node2. Node1 and Node2 compute the private key of the Root through ECDH.
The private key of the Root is the shared key among the MLS group members. Each member uses this shared key along with their respective related keys to derive their message encryption key.
The most important feature of this key tree is that child nodes know the private keys of their parent nodes.
—————————————————
If member A suspects their key has been compromised, they need to update their key.
Member A generates a new key pair  (public key and private key) locally and recalculates the keys for Node3’, Node1’, and Root’.
Then, A encrypts the public keys of Node3’ and Node1’ using the old public keys of Node3 and Node1, respectively, and sends them to all group members.
When member H receives and decrypts the message, they obtain the public key of Node1’ and, combined with the private key of Node2, perform an ECDH computation to calculate the new private key of Root’.
Other members perform similar operations. As a result, all members successfully update the key tree.
The advantage of the MLS protocol is that when a member updates their key, the complexity of updating the key tree is reduced to O(logN).
Imagine if there were no binary tree. When A updates their key, they would need to update the message one-to-one for each group member, resulting in a complexity of O(N).
However, if member B’s key is compromised, member A updating their key cannot rescue member B. Each member’s update key operation can only protect themselves, not all members.

The MLS group members (A, B, C, D, E, F, G, H) form the leaf nodes of a binary tree as shown below. Each member has a pair of public and private keys.
For member A, they use their private key  and member B’s public key  to perform an ECDH computation. For member B, they use their private key  and member A’s public key  to perform an ECDH computation.
Both compute the same value. This value becomes the private key of Node3, and from this, the public key of Node3 can also be derived.
Similarly, other members perform their respective ECDH computations.
Moreover, nodes higher in the tree also perform their respective ECDH computations up to the Root. Node3 and Node4 compute the private key of Node1 through ECDH, while Node5 and Node6 compute the private key of Node2. Node1 and Node2 compute the private key of the Root through ECDH.
The private key of the Root is the shared key among the MLS group members. Each member uses this shared key along with their respective related keys to derive their message encryption key.
The most important feature of this key tree is that child nodes know the private keys of their parent nodes.
—————————————————
If member A suspects their key has been compromised, they need to update their key.
Member A generates a new key pair  (public key and private key) locally and recalculates the keys for Node3’, Node1’, and Root’.
Then, A encrypts the public keys of Node3’ and Node1’ using the old public keys of Node3 and Node1, respectively, and sends them to all group members.
When member H receives and decrypts the message, they obtain the public key of Node1’ and, combined with the private key of Node2, perform an ECDH computation to calculate the new private key of Root’.
Other members perform similar operations. As a result, all members successfully update the key tree.
The advantage of the MLS protocol is that when a member updates their key, the complexity of updating the key tree is reduced to O(logN).
Imagine if there were no binary tree. When A updates their key, they would need to update the message one-to-one for each group member, resulting in a complexity of O(N).
However, if member B’s key is compromised, member A updating their key cannot rescue member B. Each member’s update key operation can only protect themselves, not all members.


quoting note1guz…mq8y7/n
The MLS (Messaging Layer Security) group's central feature is its efficiency in updating both group members and the shared root key, reducing the number of necessary communications from N individual chats down to log2(N).
Consider the MLS group as an evolution of the upgraded sender key group, with a similar mechanism for deriving encryption keys from a root key at the top of a hierarchy.
Imagine a scenario where a group member, A, believes their key has been compromised and needs an update. This would trigger an update of the root key. But the challenge is how A informs the rest of the group about this change.
In an upgraded sender key group, A would have to individually communicate with every other member, resulting in N-1 private messages.
The MLS group, however, is structured around a key tree. The leaves of this tree represent the group members—A through H—with the root key at the very top. A distinctive feature of this structure is that each child node has access to its parent node’s private key.
For instance, A can update E, F, G, and H by sending a single message encrypted with the public key of node 1. Since these members are the children of node 1 and possess its private key, they can decrypt the message.
Similarly, A can inform C and D by encrypting a message with the public key of node 2, to which they, being children of node 2, have the private key and can thus decrypt.
A directly communicates the update to B with one personal message.
In total, A needs to send log2(8) = 3 messages to update the entire group.
If the group size were as large as 1024 members, A would only need to send log2(1024) = 10 messages.
This efficient mechanism of updating members and the root key grants the MLS group the backward secrecy feature, an enhancement over capabilities found in the upgraded sender key group.
We are studying the MLS protocol and will implement the MLS group feature in Keychat later.