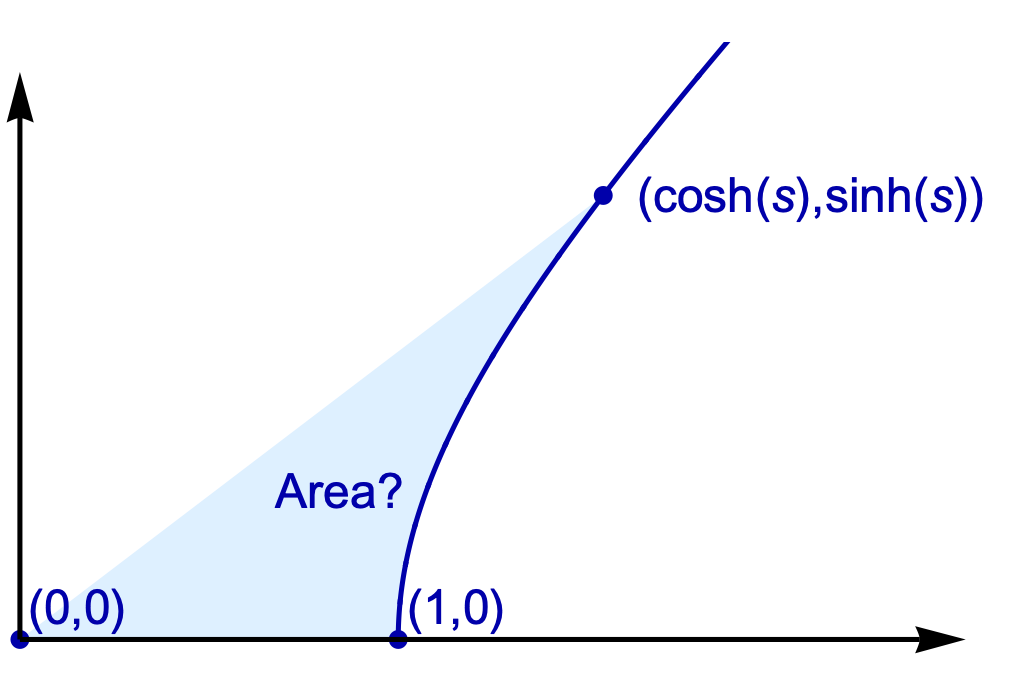
Greg Egan on Nostr: The blue curve here is the “unit hyperbola” traced out by points of the form ...
The blue curve here is the “unit hyperbola” traced out by points of the form (cosh(s), sinh(s)). There are a few different ways we could compute the area of the light blue wedge, but this might be the most fun:
If instead we had a circle traced out by (cos(s), sin(s)), then the equivalent wedge, a sector of a circle, would simply have area ½s.
And if the hyperbola was a world line in a spacetime diagram for a relativistic traveller, every point on it would lie at a proper distance of 1 from the origin, and the parameter s would be elapsed proper time as measured by the traveller. The area in spacetime swept out to form the wedge would again be simply ½s.
But although the distances and angles in a spacetime diagram drawn in ordinary space are *not* the true, relativistic distances and angles of Lorentzian spacetime geometry, areas *are* identical!
So even in ordinary Euclidean space, the area of the light blue wedge is just ½s.
H/T https://bsky.app/profile/omershapira.com/post/3ld56a5mldc2e
If instead we had a circle traced out by (cos(s), sin(s)), then the equivalent wedge, a sector of a circle, would simply have area ½s.
And if the hyperbola was a world line in a spacetime diagram for a relativistic traveller, every point on it would lie at a proper distance of 1 from the origin, and the parameter s would be elapsed proper time as measured by the traveller. The area in spacetime swept out to form the wedge would again be simply ½s.
But although the distances and angles in a spacetime diagram drawn in ordinary space are *not* the true, relativistic distances and angles of Lorentzian spacetime geometry, areas *are* identical!
So even in ordinary Euclidean space, the area of the light blue wedge is just ½s.
H/T https://bsky.app/profile/omershapira.com/post/3ld56a5mldc2e
