chontit on Nostr: 🙋♂️ ECDSA ฉบับเตรียมสอบ‼️ #Siamstr ...
🙋♂️ ECDSA ฉบับเตรียมสอบ‼️ #Siamstr
❗️ทุกคนที่ผ่านการร่ำเรียนในระดับชั้นต่าง ๆ มาคงรู้ใช่มั้ยครับว่าก่อนสอบจะมีเพื่อนมาปล่อยโผ!! ซึ่งมันคือข้อมูลที่นำไปใช้สอบเพื่อ 'ผ่าน' แต่คงไม่มีทางเข้าใจอย่างถ่องแท้จากแค่โผแน่ ๆ 5555 😊
✅วันนี้ผมก็ขอลองปล่อยโผ ECDSA ให้เพื่อน ๆ ลองอ่านเล่น ๆ กันนะครับ เผื่อต้องไปตอบคำถามป้าข้างบ้านว่าทำไม Bitcoin Address มันถึงคำนวนย้อนกลับไปหา Private Key ไม่ได้ 🤔
.
➡️ เริ่มต้นด้วยทฤษฎีก่อน ,, ECDSA ย่อมาจาก Elliptic Curve Digital Signature Algorithm โดยในตัวบิตคอยน์เนี่ย.. มันใช้ Parameters secp256k1 ซึ่งในรายละเอียดมันคืออะไรนั้น .. ช่างมันเถอะนะ 😎
เอาเป็นว่า...
✅ มันคือกล่องสี่เหลี่ยมที่เต็มไปด้วยจุดตัวเลขจำนวนเต็มพิกัด x,y ต่าง ๆ 'จำนวนมหาศาล' ,, ถ้าจินตนาการไม่ออกว่ามันเยอะแค่ไหนลองดูภาพประกอบด้านล่างได้
➡️ ค่า x และ y ที่เป็นไปได้ คือ จำนวนเต็มที่มีค่าระหว่าง 0 ถึง 1.15792 x 10^77 หรือประมาณ "หนึ่งแสน หนึ่งหมื่น ห้าพัน เจ็ดร้อย เก้าสิบ สอง ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน" ตัวเลขเท่านั้นเอง 😇
➡️ ค่า x, y ทุก ๆ ค่าจะเป็นไปตามสมการ y^2 mod p = x^3 + 7 mod p (ใคร งง ตรงนี้ข้ามไปได้เลย ,, ไว้วันที่กินเบียร์งาน Meetup เดี๋ยวเล่าให้ฟัง) 👍
.
❗️ทีนี้เรามาเข้าเรื่องกันเลยดีกว่า ทำไมเราถึงไม่สามารถคำนวนย้อนกลับจาก Bitcoin Address ไปหา Private Key ได้ ? ลองดูในรูปประกอบนะฮะ ,, ซึ่งเป็นตัวอย่างการคำนวนแค่ 5G เพื่อให้เข้าใจง่ายและเห็นภาพเท่านั้นเอง
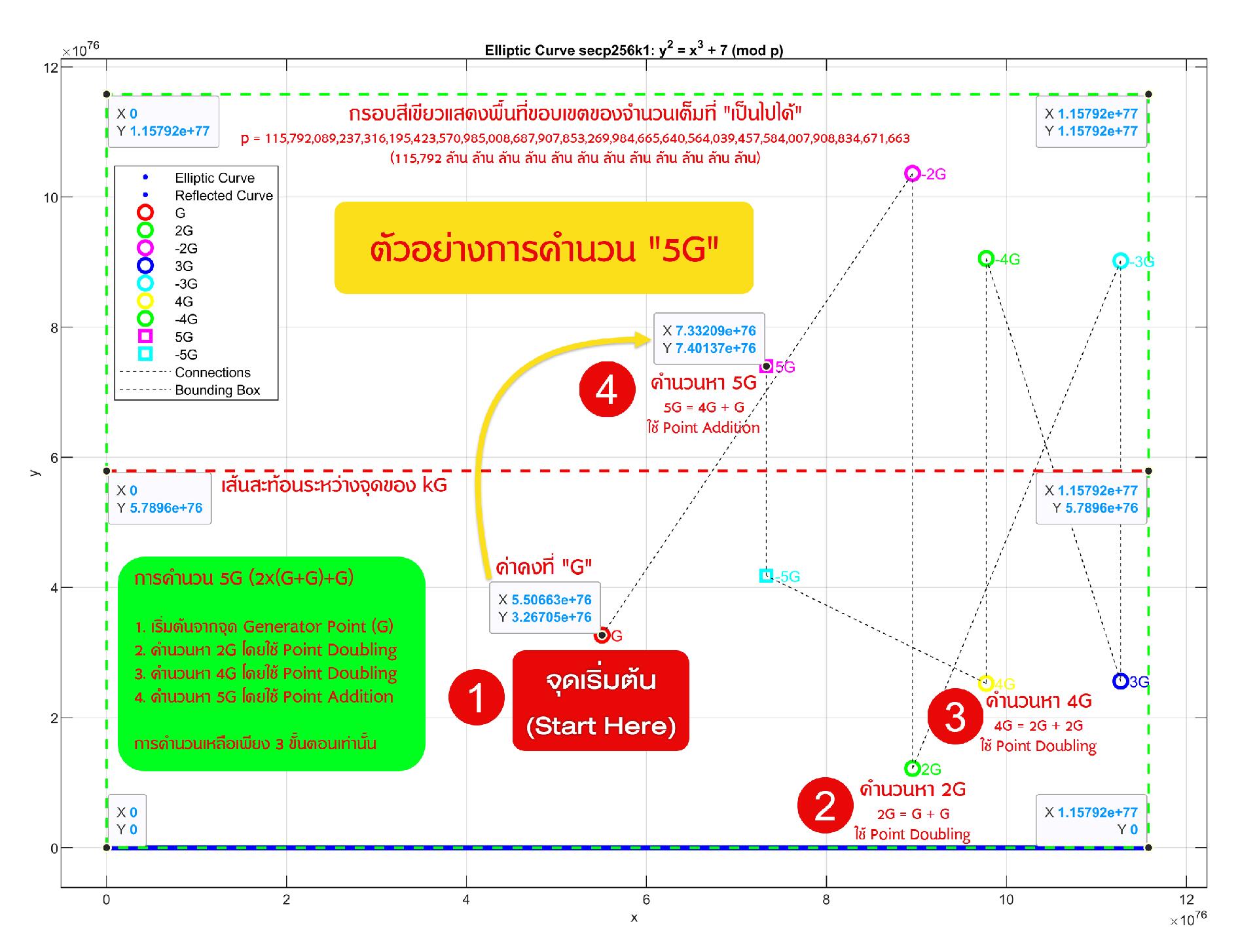
➡️ เริ่มต้นจากจุด G หรือเป็นค่าคงที่ที่กำหนดไว้แล้ว เรียกว่า Generator Point (หมายเลข 1 ในภาพประกอบ)
1️⃣ จากนั้นคำนวนหา 2G (2G = G+G) ซึ่ง..มันมีสมการคำนวนแหละ แต่ยังไม่ต้องรู้หรอก ,, เอาเป็นว่า เราจะได้จุด 2G ตามหมายเลข 2 ในภาพประกอบ
2️⃣ จากนั้นคำนวนหาจุด 4G ซึ่งเราจะใช้ข้อมูลจากจุด 2G มาคำนวน (4G = 2G + 2G) ทำให้การคำนวนรวดเร็วมากขึ้น (เร็วกว่า 4G = G+G+G+G)
3️⃣ สุดท้ายก็จะนำค่าพิกัด x,y ที่จุด 4G มาบวกกับค่า G ก็จะได้พิกัดของจุด 5G ตามต้องการ เย้ 🎉
✅ แต่ถ้าเราต้องการ 10G ล่ะ ? ใช่แล้วแหละ เราก็จะคำนวนจาก 10G = 5G+5G ก็จะได้ตำแหน่งของ 10G ทันที ,, และเช่นเดียวกัน ถ้าเราต้องการตำแหน่ง 100G เราก็จะใช้วิธีการบวกทบ ๆ กันไปเรื่อย ๆ ตามตัวอย่างแบบที่อธิบายแหละ 👍
.
🙋♂️ ดูแล้วก็ไม่น่ายากนี่น่า.. งั้นลองคิดกลับกัน
‼️ถ้าเรารู้พิกัด x = 7.33209 x 10^76 และ y = 7.40137 x 10^76 ,, เราจะสามารถหา 'จำนวนตัวเลข' ที่มาคูนกับ G แล้วผลลัพธ์เป็นพิกัดดังกล่าวได้มั้ยนะ ? 🤔
✅ ใช่แล้ว.... มันไม่มีสมการคำนวนย้อนกลับ ,, เพราะฉะนั้น เราไม่มีทางรู้ว่า 'ตัวเลข' ไหนที่นำมาคำนวนกับค่า G แล้วจะได้ผลลัพธ์นั้นแบบ 'พอดีเป๊ะ ๆ' นอกจากว่าจะลองคำนวนจาก G+G+G+G..... ไปเรื่อย ๆ จนกว่าจะเจอตัวเลขที่ต้องการ 👍
.
❗แต่ Bitcoin Address มันไม่ได้คำนวนจากตัวเลขน้อย ๆ แค่ 5G เหมือนที่ผมสาธิตหน่ะสิ
‼️ตัวเลขจำนวนเต็มที่ใช้คูนกับค่า G มันก็คือ 'Private Key' นั่นเอง
➡️ สมมุติว่า Private Key = 0000000000000000000000000000000000000000000000000DE0B6B3A7640000
➡️ เมื่อแปลงเป็นเลขฐาน 10 คือ 1,000,000,000,000,000,000 (1 ล้าน ล้าน ล้าน)
นั่นหมายความว่า ...
✅ กระบวนการ kG ก็คือ การบวกค่า G เรื่อย ๆ ทั้งหมด '1 ล้าน ล้าน ล้าน' ครั้ง ,, แล้วผลลัพธ์ที่ได้จะถูกนำไปใช้คำนวนหา Public Key ต่อไป (ผลลัพธ์ยังไม่ใช่ Bitcoin Address นะฮะ ,, การได้ Bitcoin Address ที่เราใช้งานกันยังต้องผ่านกระบวนการเพิ่มเติมอีกเล็กน้อย)
🙋♂️ รู้แบบนี้แล้ว… ยังจะมีใครลองพยายามคำนวน Public Key กลับไปเป็น Private Key อยู่อีกมั้ยนะ ? 😘
.
❗ทิ้งท้ายไว้อีกนิด เผื่อมีคนสงสัยว่า…ถ้าเราใช้วิธีการ 'สุ่ม' ไปเรื่อย ๆ หรือ Brute Force ทำได้มั้ย ? 🤔
✅ ขอตอบว่า ‘ทำได้แน่นอน’ แต่...ชาตินี้คุณมีเวลาชีวิตพอหรือป่าวล่ะ ?
➡️ ยกตัวอย่าง Private Key ด้านบน ,, คุณใช้คอมพิวเตอร์ที่สามารถสุ่มได้ 1 ล้านรหัสต่อวินาที (โคตรเร็ว) 😱
➡️ คุณต้องใช้เวลาอีก 1 ล้าน ล้าน วินาที ในการสุ่มจนกว่าจะเจอ Private Key (ประมาณ 11,574,074 วัน หรือ 31,709 ปี) 🥶
.
🙋♂️ พอเห็นภาพกันมั้ยครับ ? ว่า..
🧡 'บิตคอยน์' เป็นระบบการเงินที่โคตรของโคตรปลอดภัยในปัจจุบันนี้เลย
ป.ล.ภาพประกอบผมใช้ Matlab สร้างกราฟให้ครับ ,, ส่วนผลลัพธ์การคำนวนแต่ละจุดให้ ChatGPT ช่วย ,, ตัวเลขอาจจะตรงบ้างไม่ตรงบ้าง แต่โดยหลักการแล้วถูกต้องตามนี้ 😇🙏
#เวลามีค่าศึกษาบิตคอยน์
#Siamstr
❗️ทุกคนที่ผ่านการร่ำเรียนในระดับชั้นต่าง ๆ มาคงรู้ใช่มั้ยครับว่าก่อนสอบจะมีเพื่อนมาปล่อยโผ!! ซึ่งมันคือข้อมูลที่นำไปใช้สอบเพื่อ 'ผ่าน' แต่คงไม่มีทางเข้าใจอย่างถ่องแท้จากแค่โผแน่ ๆ 5555 😊
✅วันนี้ผมก็ขอลองปล่อยโผ ECDSA ให้เพื่อน ๆ ลองอ่านเล่น ๆ กันนะครับ เผื่อต้องไปตอบคำถามป้าข้างบ้านว่าทำไม Bitcoin Address มันถึงคำนวนย้อนกลับไปหา Private Key ไม่ได้ 🤔
.
➡️ เริ่มต้นด้วยทฤษฎีก่อน ,, ECDSA ย่อมาจาก Elliptic Curve Digital Signature Algorithm โดยในตัวบิตคอยน์เนี่ย.. มันใช้ Parameters secp256k1 ซึ่งในรายละเอียดมันคืออะไรนั้น .. ช่างมันเถอะนะ 😎
เอาเป็นว่า...
✅ มันคือกล่องสี่เหลี่ยมที่เต็มไปด้วยจุดตัวเลขจำนวนเต็มพิกัด x,y ต่าง ๆ 'จำนวนมหาศาล' ,, ถ้าจินตนาการไม่ออกว่ามันเยอะแค่ไหนลองดูภาพประกอบด้านล่างได้
➡️ ค่า x และ y ที่เป็นไปได้ คือ จำนวนเต็มที่มีค่าระหว่าง 0 ถึง 1.15792 x 10^77 หรือประมาณ "หนึ่งแสน หนึ่งหมื่น ห้าพัน เจ็ดร้อย เก้าสิบ สอง ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน ล้าน" ตัวเลขเท่านั้นเอง 😇
➡️ ค่า x, y ทุก ๆ ค่าจะเป็นไปตามสมการ y^2 mod p = x^3 + 7 mod p (ใคร งง ตรงนี้ข้ามไปได้เลย ,, ไว้วันที่กินเบียร์งาน Meetup เดี๋ยวเล่าให้ฟัง) 👍
.
❗️ทีนี้เรามาเข้าเรื่องกันเลยดีกว่า ทำไมเราถึงไม่สามารถคำนวนย้อนกลับจาก Bitcoin Address ไปหา Private Key ได้ ? ลองดูในรูปประกอบนะฮะ ,, ซึ่งเป็นตัวอย่างการคำนวนแค่ 5G เพื่อให้เข้าใจง่ายและเห็นภาพเท่านั้นเอง

➡️ เริ่มต้นจากจุด G หรือเป็นค่าคงที่ที่กำหนดไว้แล้ว เรียกว่า Generator Point (หมายเลข 1 ในภาพประกอบ)
1️⃣ จากนั้นคำนวนหา 2G (2G = G+G) ซึ่ง..มันมีสมการคำนวนแหละ แต่ยังไม่ต้องรู้หรอก ,, เอาเป็นว่า เราจะได้จุด 2G ตามหมายเลข 2 ในภาพประกอบ
2️⃣ จากนั้นคำนวนหาจุด 4G ซึ่งเราจะใช้ข้อมูลจากจุด 2G มาคำนวน (4G = 2G + 2G) ทำให้การคำนวนรวดเร็วมากขึ้น (เร็วกว่า 4G = G+G+G+G)
3️⃣ สุดท้ายก็จะนำค่าพิกัด x,y ที่จุด 4G มาบวกกับค่า G ก็จะได้พิกัดของจุด 5G ตามต้องการ เย้ 🎉
✅ แต่ถ้าเราต้องการ 10G ล่ะ ? ใช่แล้วแหละ เราก็จะคำนวนจาก 10G = 5G+5G ก็จะได้ตำแหน่งของ 10G ทันที ,, และเช่นเดียวกัน ถ้าเราต้องการตำแหน่ง 100G เราก็จะใช้วิธีการบวกทบ ๆ กันไปเรื่อย ๆ ตามตัวอย่างแบบที่อธิบายแหละ 👍
.
🙋♂️ ดูแล้วก็ไม่น่ายากนี่น่า.. งั้นลองคิดกลับกัน
‼️ถ้าเรารู้พิกัด x = 7.33209 x 10^76 และ y = 7.40137 x 10^76 ,, เราจะสามารถหา 'จำนวนตัวเลข' ที่มาคูนกับ G แล้วผลลัพธ์เป็นพิกัดดังกล่าวได้มั้ยนะ ? 🤔
✅ ใช่แล้ว.... มันไม่มีสมการคำนวนย้อนกลับ ,, เพราะฉะนั้น เราไม่มีทางรู้ว่า 'ตัวเลข' ไหนที่นำมาคำนวนกับค่า G แล้วจะได้ผลลัพธ์นั้นแบบ 'พอดีเป๊ะ ๆ' นอกจากว่าจะลองคำนวนจาก G+G+G+G..... ไปเรื่อย ๆ จนกว่าจะเจอตัวเลขที่ต้องการ 👍
.
❗แต่ Bitcoin Address มันไม่ได้คำนวนจากตัวเลขน้อย ๆ แค่ 5G เหมือนที่ผมสาธิตหน่ะสิ
‼️ตัวเลขจำนวนเต็มที่ใช้คูนกับค่า G มันก็คือ 'Private Key' นั่นเอง
➡️ สมมุติว่า Private Key = 0000000000000000000000000000000000000000000000000DE0B6B3A7640000
➡️ เมื่อแปลงเป็นเลขฐาน 10 คือ 1,000,000,000,000,000,000 (1 ล้าน ล้าน ล้าน)
นั่นหมายความว่า ...
✅ กระบวนการ kG ก็คือ การบวกค่า G เรื่อย ๆ ทั้งหมด '1 ล้าน ล้าน ล้าน' ครั้ง ,, แล้วผลลัพธ์ที่ได้จะถูกนำไปใช้คำนวนหา Public Key ต่อไป (ผลลัพธ์ยังไม่ใช่ Bitcoin Address นะฮะ ,, การได้ Bitcoin Address ที่เราใช้งานกันยังต้องผ่านกระบวนการเพิ่มเติมอีกเล็กน้อย)
🙋♂️ รู้แบบนี้แล้ว… ยังจะมีใครลองพยายามคำนวน Public Key กลับไปเป็น Private Key อยู่อีกมั้ยนะ ? 😘
.
❗ทิ้งท้ายไว้อีกนิด เผื่อมีคนสงสัยว่า…ถ้าเราใช้วิธีการ 'สุ่ม' ไปเรื่อย ๆ หรือ Brute Force ทำได้มั้ย ? 🤔
✅ ขอตอบว่า ‘ทำได้แน่นอน’ แต่...ชาตินี้คุณมีเวลาชีวิตพอหรือป่าวล่ะ ?
➡️ ยกตัวอย่าง Private Key ด้านบน ,, คุณใช้คอมพิวเตอร์ที่สามารถสุ่มได้ 1 ล้านรหัสต่อวินาที (โคตรเร็ว) 😱
➡️ คุณต้องใช้เวลาอีก 1 ล้าน ล้าน วินาที ในการสุ่มจนกว่าจะเจอ Private Key (ประมาณ 11,574,074 วัน หรือ 31,709 ปี) 🥶
.
🙋♂️ พอเห็นภาพกันมั้ยครับ ? ว่า..
🧡 'บิตคอยน์' เป็นระบบการเงินที่โคตรของโคตรปลอดภัยในปัจจุบันนี้เลย
ป.ล.ภาพประกอบผมใช้ Matlab สร้างกราฟให้ครับ ,, ส่วนผลลัพธ์การคำนวนแต่ละจุดให้ ChatGPT ช่วย ,, ตัวเลขอาจจะตรงบ้างไม่ตรงบ้าง แต่โดยหลักการแล้วถูกต้องตามนี้ 😇🙏
#เวลามีค่าศึกษาบิตคอยน์
#Siamstr
