Greg Egan on Nostr: If a geodesic (the blue curve) has an inflection point (the black dot), then its ...
If a geodesic (the blue curve) has an inflection point (the black dot), then its tangent must be pointing in one of the “asymptotic directions” of the surface at that point: a direction such that all curves have a normal curvature here of zero. So, the geodesic will share its tangent with an asymptotic curve (the black curve, https://en.wikipedia.org/wiki/Asymptotic_curve).
The asymptotic curve has its curvature vector orthogonal to the normal to the surface, whereas the geodesic, though it has a zero curvature vector at the point itself, has a principal normal vector (the unit vector parallel or antiparallel to the curvature vector, extended by continuity across inflection points) that is parallel or antiparallel to the normal to the surface. So, the instantaneous planes in which the two curves lie are momentarily locked together, at a right angle to each other. This means the torsion, the rate at which those planes rotate, must be the same (or opposite) at this point.
But there is a theorem of Beltrami and Enneper which says that the torsion τ of an asymptotic curve obeys τ^2 = –K, where K is the Gaussian curvature. So if K=–1, τ=±1 for both the asymptotic curve (all along its length), and for the geodesic (at this point).
The theorem is proved in some textbooks on the subject (e.g. “Differential Geometry”, Martin Lipschutz, Theorem 9.18), but I also give a proof here in the context of the sine-Gordon equation: https://www.gregegan.net/SCIENCE/PSP/PSP.html#SG
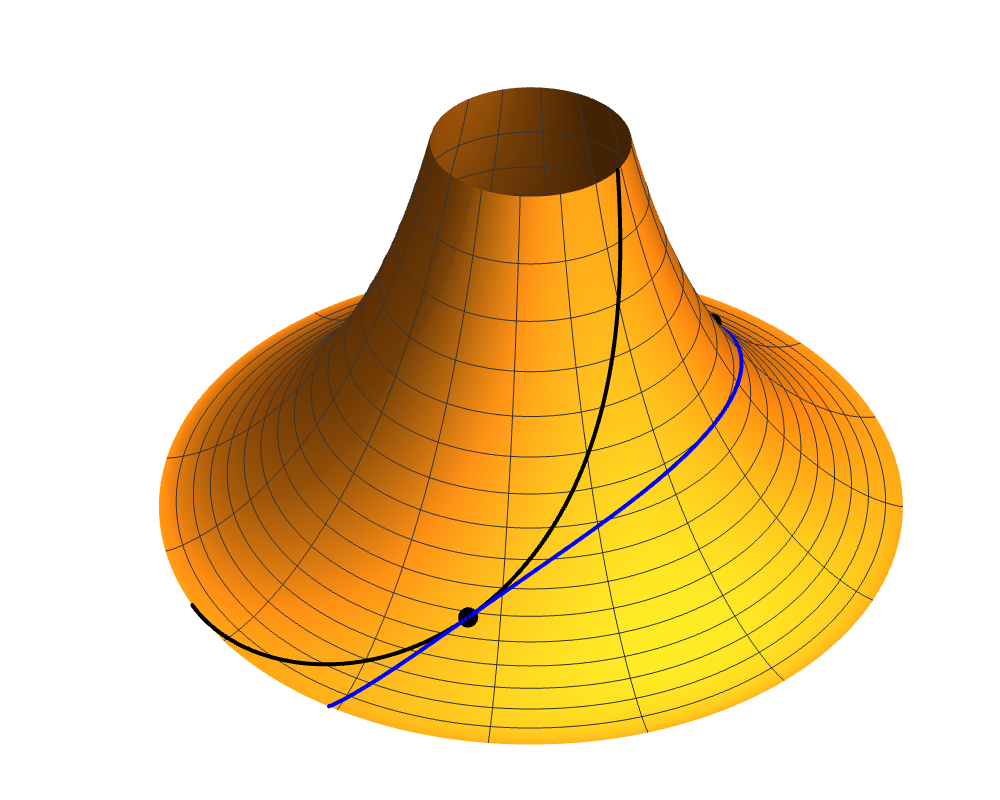
The asymptotic curve has its curvature vector orthogonal to the normal to the surface, whereas the geodesic, though it has a zero curvature vector at the point itself, has a principal normal vector (the unit vector parallel or antiparallel to the curvature vector, extended by continuity across inflection points) that is parallel or antiparallel to the normal to the surface. So, the instantaneous planes in which the two curves lie are momentarily locked together, at a right angle to each other. This means the torsion, the rate at which those planes rotate, must be the same (or opposite) at this point.
But there is a theorem of Beltrami and Enneper which says that the torsion τ of an asymptotic curve obeys τ^2 = –K, where K is the Gaussian curvature. So if K=–1, τ=±1 for both the asymptotic curve (all along its length), and for the geodesic (at this point).
The theorem is proved in some textbooks on the subject (e.g. “Differential Geometry”, Martin Lipschutz, Theorem 9.18), but I also give a proof here in the context of the sine-Gordon equation: https://www.gregegan.net/SCIENCE/PSP/PSP.html#SG
