John Carlos Baez on Nostr: Did you ever think of music as 2-dimensional? • Following a red arrow, the ...
Did you ever think of music as 2-dimensional?
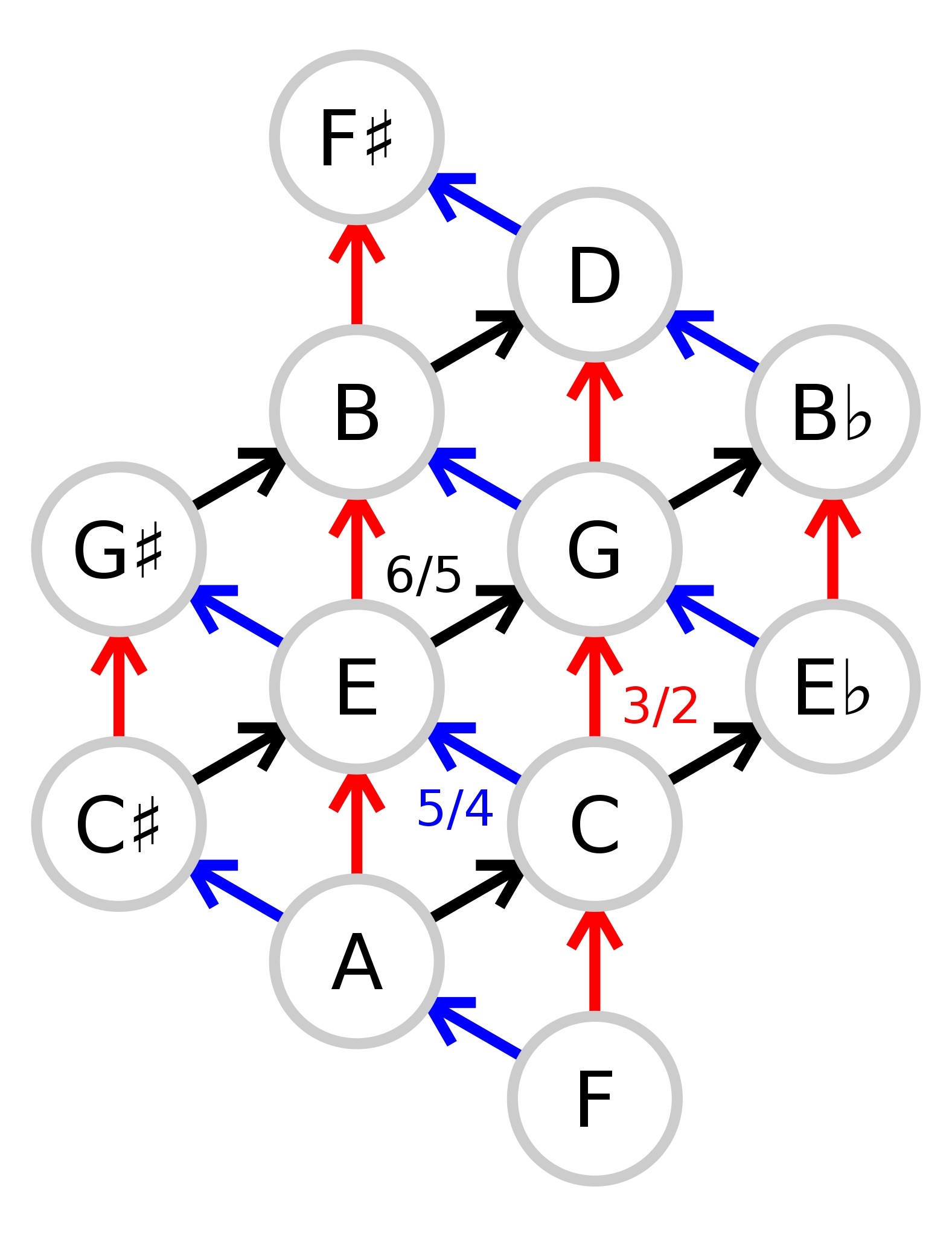
• Following a red arrow, the frequency goes up by a factor of 3/2 (called a perfect fifth).
• Following a blue arrow, the frequency goes up by a factor of 5/4 (called a major third).
• Following a black arrow, the frequency goes up by a factor of 6/5 (called a minor third).
This setup is used for some keyboards - like on accordions - but it's also useful in '5-limit tuning', where frequency ratios only involve powers of 2, 3, and 5. Just intonation, which I talked about yesterday:
https://mathstodon.xyz/@johncarlosbaez/111170247654517571
is the best known 5-limit tuning system. But there are others!
We often use logarithms to turn frequency ratios into numbers we can add instead of multiply. Since ln(2), ln(3) and ln(5) are linearly independent over the rational numbers, the numbers ln(2ⁱ3ʲ5ᵏ) actually form a 3-dimensional structure: mathematicians call it a free abelian group of rank 3. This chart just shows a 2-dimensonal 'slice' of that.
For example, following the arrows on this chart (which extends indefinitely) you'll never get a note with exactly 2 times the frequency of your starting note. That means you never get a perfect octave! 😿
But the perfect octave does lurk in the 3-dimensional structure of which this chart is a slice.
• Following a red arrow, the frequency goes up by a factor of 3/2 (called a perfect fifth).
• Following a blue arrow, the frequency goes up by a factor of 5/4 (called a major third).
• Following a black arrow, the frequency goes up by a factor of 6/5 (called a minor third).
This setup is used for some keyboards - like on accordions - but it's also useful in '5-limit tuning', where frequency ratios only involve powers of 2, 3, and 5. Just intonation, which I talked about yesterday:
https://mathstodon.xyz/@johncarlosbaez/111170247654517571
is the best known 5-limit tuning system. But there are others!
We often use logarithms to turn frequency ratios into numbers we can add instead of multiply. Since ln(2), ln(3) and ln(5) are linearly independent over the rational numbers, the numbers ln(2ⁱ3ʲ5ᵏ) actually form a 3-dimensional structure: mathematicians call it a free abelian group of rank 3. This chart just shows a 2-dimensonal 'slice' of that.
For example, following the arrows on this chart (which extends indefinitely) you'll never get a note with exactly 2 times the frequency of your starting note. That means you never get a perfect octave! 😿
But the perfect octave does lurk in the 3-dimensional structure of which this chart is a slice.
