John Carlos Baez on Nostr: In Pythagorean tuning, we try to force all frequency ratios to be powers of 3/2. In ...
In Pythagorean tuning, we try to force all frequency ratios to be powers of 3/2. In music, 3/2 is the 'perfect fifth': the sweetest of intervals except for the octave.
If we start with some frequency and go up and down by powers of 3/2, we create the 'circle of fifths' shown here. It's almost a 12-pointed star, with one point for each note in the 12-tone equal-tempered scale.
Almost - but not quite! When we go up 12 perfect fifths, we get a note that's almost but not quite 2⁷ times the frequency we started with. In other words, it's almost but not quite 7 octaves higher. So there's a glitch.
Here I've stuck that glitch at the opposite from the note labeled 1. The spot directly opposite 1 is called the 'tritone', or sometimes 'diabolus in musica' - the devil in music. 😈
The size of the glitch is called the 'Pythagorean comma'. It's
(3/2)¹² / 2⁷ ≈ 129.74633789 / 128 ≈ 1.01364326477
https://en.wikipedia.org/wiki/Pythagorean_tuning
https://en.wikipedia.org/wiki/Pythagorean_comma
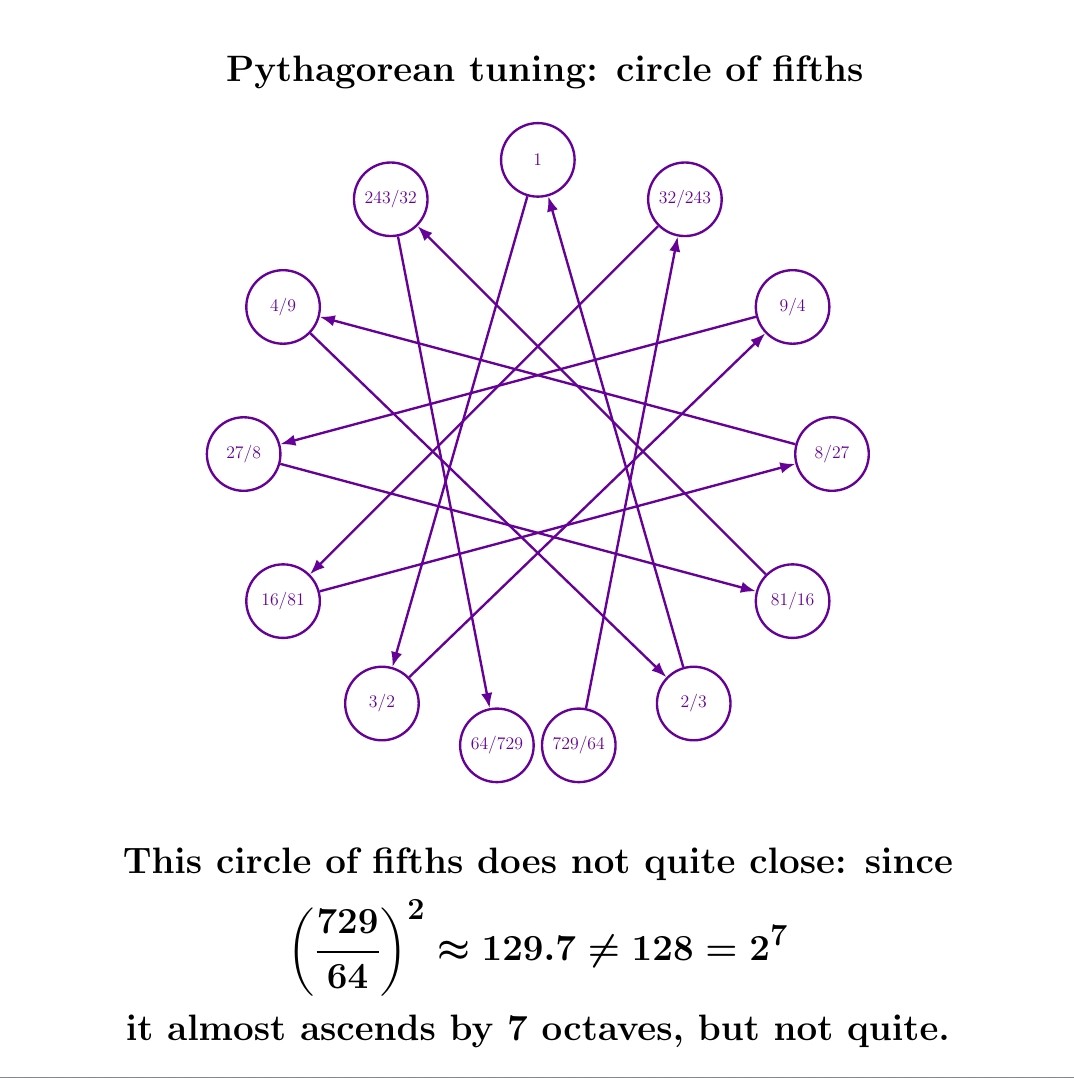
If we start with some frequency and go up and down by powers of 3/2, we create the 'circle of fifths' shown here. It's almost a 12-pointed star, with one point for each note in the 12-tone equal-tempered scale.
Almost - but not quite! When we go up 12 perfect fifths, we get a note that's almost but not quite 2⁷ times the frequency we started with. In other words, it's almost but not quite 7 octaves higher. So there's a glitch.
Here I've stuck that glitch at the opposite from the note labeled 1. The spot directly opposite 1 is called the 'tritone', or sometimes 'diabolus in musica' - the devil in music. 😈
The size of the glitch is called the 'Pythagorean comma'. It's
(3/2)¹² / 2⁷ ≈ 129.74633789 / 128 ≈ 1.01364326477
https://en.wikipedia.org/wiki/Pythagorean_tuning
https://en.wikipedia.org/wiki/Pythagorean_comma
