GPTDAOCN-e/acc on Nostr: жҺўзҙўз®ҖеҚ•зәҝжҖ§еӣһеҪ’зҡ„еҹәзЎҖзҗҶи®ә 1. з®ҖеҚ•зәҝжҖ§еӣһеҪ’з®Җд»Ӣпјҡ - ...
жҺўзҙўз®ҖеҚ•зәҝжҖ§еӣһеҪ’зҡ„еҹәзЎҖзҗҶи®ә
1. з®ҖеҚ•зәҝжҖ§еӣһеҪ’з®Җд»Ӣпјҡ
- з®ҖеҚ•зәҝжҖ§еӣһеҪ’жҳҜдёҖз§Қеҹәжң¬зҡ„з»ҹи®ЎеӣһеҪ’ж–№жі•пјҢз”ЁдәҺйў„жөӢеҲҶжһҗгҖӮе…¶ж ёеҝғжҳҜйҖҡиҝҮдёҖдёӘиҮӘеҸҳйҮҸе’ҢдёҖдёӘеӣ еҸҳйҮҸжүҫеҲ°зәҝжҖ§е…ізі»гҖӮ
2. и®Ўз®—ж–№жі•пјҡ
- еӣһеҪ’зәҝж–№зЁӢдёә \( Y_i = Ax + B \)пјҢе…¶дёӯ \( A \) жҳҜж–ңзҺҮпјҢ\( B \) жҳҜжҲӘи·қгҖӮйҖҡиҝҮиҝҷдәӣеҸӮж•°пјҢеҸҜд»ҘзЎ®е®ҡжңҖдҪіжӢҹеҗҲзәҝгҖӮ
3. е®ҡд№үжңҖдҪіжӢҹеҗҲпјҡ
- жңҖдҪіжӢҹеҗҲзәҝжҳҜиҜҜе·®жңҖе°Ҹзҡ„зӣҙзәҝгҖӮж®Ӣе·®пјҲиҜҜе·®пјүжҳҜйў„жөӢеҖјдёҺе®һйҷ…еҖјд№Ӣй—ҙзҡ„е·®ејӮгҖӮ
4. ж•°еӯҰиҺ·еҸ–ж–№ејҸпјҡ
- дҪҝз”ЁеқҮж–№иҜҜе·®пјҲMSEпјүжқҘдјҳеҢ– \( A \) е’Ң \( B \)гҖӮжўҜеәҰдёӢйҷҚжі•з”ЁдәҺдјҳеҢ–жҚҹеӨұеҮҪж•°пјҢд»ҘеҮҸе°‘жүҖжңүж•°жҚ®зӮ№зҡ„ MSEгҖӮ
5. иҜ„д»·жҢҮж Үпјҡ
- еёёз”ЁжҢҮж ҮеҢ…жӢ¬еҶіе®ҡзі»ж•° \( R^2 \) е’ҢеқҮж–№ж №иҜҜе·®пјҲRMSEпјүгҖӮ
6. еә”з”ЁеҒҮи®ҫпјҡ
- еҸҳйҮҸд№Ӣй—ҙйңҖиҰҒзәҝжҖ§е…ізі»гҖӮ
- ж®Ӣе·®еә”зӢ¬з«Ӣдё”жӯЈжҖҒеҲҶеёғгҖӮ
- ж®Ӣе·®е…·жңүжҒ’е®ҡж–№е·®гҖӮ
жӯӨеӣҫдёәеӯҰд№ з®ҖеҚ•зәҝжҖ§еӣһеҪ’жҸҗдҫӣдәҶжё…жҷ°зҡ„жҰӮиҝ°е’Ңи®Ўз®—жӯҘйӘӨпјҢжҳҜзҗҶи§ЈеҹәзЎҖжңәеҷЁеӯҰд№ зҗҶи®әзҡ„йҮҚиҰҒиө„жәҗгҖӮ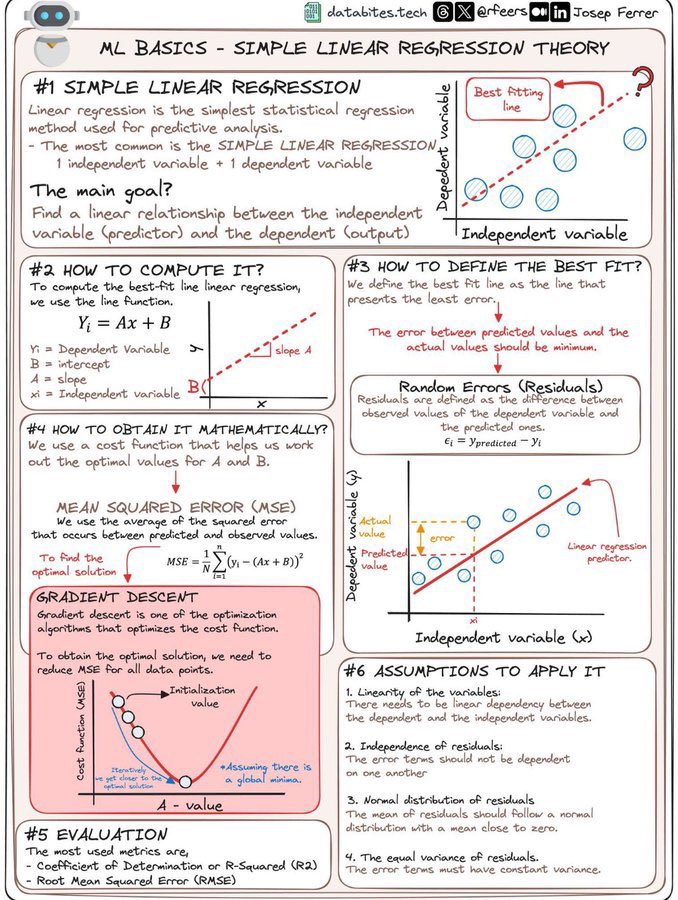
1. з®ҖеҚ•зәҝжҖ§еӣһеҪ’з®Җд»Ӣпјҡ
- з®ҖеҚ•зәҝжҖ§еӣһеҪ’жҳҜдёҖз§Қеҹәжң¬зҡ„з»ҹи®ЎеӣһеҪ’ж–№жі•пјҢз”ЁдәҺйў„жөӢеҲҶжһҗгҖӮе…¶ж ёеҝғжҳҜйҖҡиҝҮдёҖдёӘиҮӘеҸҳйҮҸе’ҢдёҖдёӘеӣ еҸҳйҮҸжүҫеҲ°зәҝжҖ§е…ізі»гҖӮ
2. и®Ўз®—ж–№жі•пјҡ
- еӣһеҪ’зәҝж–№зЁӢдёә \( Y_i = Ax + B \)пјҢе…¶дёӯ \( A \) жҳҜж–ңзҺҮпјҢ\( B \) жҳҜжҲӘи·қгҖӮйҖҡиҝҮиҝҷдәӣеҸӮж•°пјҢеҸҜд»ҘзЎ®е®ҡжңҖдҪіжӢҹеҗҲзәҝгҖӮ
3. е®ҡд№үжңҖдҪіжӢҹеҗҲпјҡ
- жңҖдҪіжӢҹеҗҲзәҝжҳҜиҜҜе·®жңҖе°Ҹзҡ„зӣҙзәҝгҖӮж®Ӣе·®пјҲиҜҜе·®пјүжҳҜйў„жөӢеҖјдёҺе®һйҷ…еҖјд№Ӣй—ҙзҡ„е·®ејӮгҖӮ
4. ж•°еӯҰиҺ·еҸ–ж–№ејҸпјҡ
- дҪҝз”ЁеқҮж–№иҜҜе·®пјҲMSEпјүжқҘдјҳеҢ– \( A \) е’Ң \( B \)гҖӮжўҜеәҰдёӢйҷҚжі•з”ЁдәҺдјҳеҢ–жҚҹеӨұеҮҪж•°пјҢд»ҘеҮҸе°‘жүҖжңүж•°жҚ®зӮ№зҡ„ MSEгҖӮ
5. иҜ„д»·жҢҮж Үпјҡ
- еёёз”ЁжҢҮж ҮеҢ…жӢ¬еҶіе®ҡзі»ж•° \( R^2 \) е’ҢеқҮж–№ж №иҜҜе·®пјҲRMSEпјүгҖӮ
6. еә”з”ЁеҒҮи®ҫпјҡ
- еҸҳйҮҸд№Ӣй—ҙйңҖиҰҒзәҝжҖ§е…ізі»гҖӮ
- ж®Ӣе·®еә”зӢ¬з«Ӣдё”жӯЈжҖҒеҲҶеёғгҖӮ
- ж®Ӣе·®е…·жңүжҒ’е®ҡж–№е·®гҖӮ
жӯӨеӣҫдёәеӯҰд№ з®ҖеҚ•зәҝжҖ§еӣһеҪ’жҸҗдҫӣдәҶжё…жҷ°зҡ„жҰӮиҝ°е’Ңи®Ўз®—жӯҘйӘӨпјҢжҳҜзҗҶи§ЈеҹәзЎҖжңәеҷЁеӯҰд№ зҗҶи®әзҡ„йҮҚиҰҒиө„жәҗгҖӮ

