GPTDAOCN-e/acc on Nostr: ж·ұе…Ҙи§ЈиҜ»пјҡжңәеҷЁеӯҰд№ дёӯзҡ„10еӨ§еёёз”ЁжҚҹеӨұеҮҪж•° ...
ж·ұе…Ҙи§ЈиҜ»пјҡжңәеҷЁеӯҰд№ дёӯзҡ„10еӨ§еёёз”ЁжҚҹеӨұеҮҪж•°
иҝҷеј еӣҫиЎЁеҲ—еҮәдәҶжңәеҷЁеӯҰд№ дёӯжңҖеёёз”Ёзҡ„10з§ҚжҚҹеӨұеҮҪж•°пјҢ并еҲҶдёәеӣһеҪ’е’ҢеҲҶзұ»дёӨзұ»пјҡ
еӣһеҪ’жҚҹеӨұеҮҪж•°
1. Mean Bias Error (MBE)
- жҸҸиҝ°пјҡжҚ•жҚүйў„жөӢдёӯзҡ„е№іеқҮеҒҸе·®пјҢдҪҶеҫҲе°‘з”ЁдәҺи®ӯз»ғгҖӮ
- е…¬ејҸпјҡ\[ L_{MBE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i)) \]
2. Mean Absolute Error (MAE)
- жҸҸиҝ°пјҡжөӢйҮҸйў„жөӢдёӯзҡ„з»қеҜ№е№іеқҮеҒҸе·®пјҢд№ҹз§°дёәL1жҚҹеӨұгҖӮ
- е…¬ејҸпјҡ\[ L_{MAE} = \frac{1}{N} \sum_{i=1}^{N} |y_i - f(x_i)| \]
3. Mean Squared Error (MSE)
- жҸҸиҝ°пјҡе®һйҷ…еҖјдёҺйў„жөӢеҖјд№Ӣй—ҙзҡ„е№іеқҮе№іж–№и·қзҰ»пјҢд№ҹз§°дёәL2жҚҹеӨұгҖӮ
- е…¬ејҸпјҡ\[ L_{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i))^2 \]
4. Root Mean Squared Error (RMSE)
- жҸҸиҝ°пјҡMSEзҡ„е№іж–№ж №пјҢжҚҹеӨұе’Ңеӣ еҸҳйҮҸе…·жңүзӣёеҗҢеҚ•дҪҚгҖӮ
- е…¬ејҸпјҡ\[ L_{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i))^2} \]
5. Huber Loss
- жҸҸиҝ°пјҡз»“еҗҲдәҶMSEе’ҢMAEпјҢжҳҜдёҖз§ҚеҸӮж•°еҢ–зҡ„жҚҹеӨұеҮҪж•°гҖӮ
- е…¬ејҸпјҡ
\[
L_{Huber\ loss} =
\begin{cases}
\frac{1}{2}(y_i-f(x_i))^2, & |y_i-f(x_i)| \leq \delta\\
\delta(|y_i-f(x_i)|-\frac{1}{2}\delta), & \text{otherwise}
\end{cases}
\]
6. Log Cosh Loss
- жҸҸиҝ°пјҡзұ»дјјдәҺHuber LossпјҢдҪҶйқһеҸӮж•°еҢ–пјҢи®Ўз®—дёҠиҫғжҳӮиҙөгҖӮ
- е…¬ејҸпјҡ\[ L_{Log\ Cosh} = \frac{1}{N} \sum_{i=1}^{N} log(cosh(f(x_i) - y_i)) \]
еҲҶзұ»жҚҹеӨұеҮҪж•°пјҲеҢ…еҗ«дәҢеҲҶзұ»е’ҢеӨҡеҲҶзұ»пјү
1. Binary Cross Entropy (BCE)
- жҸҸиҝ°пјҡз”ЁдәҺдәҢеҲҶзұ»д»»еҠЎзҡ„жҚҹеӨұеҮҪж•°гҖӮ
- е…¬ејҸпјҡ\[ L_{BCE} = -\frac{1}{N}\sum_{i=1}^{N}[y_i\cdot log(p(x_i)) + (1-y_i)\cdot log(1-p(x_i))] \]
2. Hinge Loss
- жҸҸиҝ°пјҡжғ©зҪҡй”ҷиҜҜе’ҢдёҚиҮӘдҝЎзҡ„йў„жөӢпјҢеёёз”ЁдәҺж”ҜжҢҒеҗ‘йҮҸжңәпјҲSVMпјүгҖӮ
- е…¬ејҸпјҡ\[ L_{Hinge} = max(0, 1-(f(x) \cdot y)) \]
3. Cross Entropy Loss
- жҸҸиҝ°пјҡBCEжҚҹеӨұеңЁеӨҡеҲҶзұ»дёҠзҡ„жү©еұ•гҖӮ
- е…¬ејҸпјҡ
\[
L_{CE} = -\frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{M}(y_{ij}\log(f(x_j)))
\]
пјҲе…¶дёӯ \( N: ж ·жң¬ж•°, M: зұ»еҲ«ж•° \)пјү
4. KL Divergence
- жҸҸиҝ°пјҡжңҖе°ҸеҢ–йў„жөӢжҰӮзҺҮдёҺзңҹе®һжҰӮзҺҮеҲҶеёғд№Ӣй—ҙзҡ„е·®ејӮгҖӮ
- е…¬ејҸпјҡ
\[
L_{KC} = N\sum y_i\cdot log(\frac{y_i}{f(x(i))})
\]
иҝҷдәӣжҚҹеӨұеҮҪж•°еңЁдёҚеҗҢд»»еҠЎдёӯеё®еҠ©дјҳеҢ–жЁЎеһӢжҖ§иғҪпјҢйҖүжӢ©еҗҲйҖӮзҡ„жҚҹеӨұеҮҪж•°еҜ№жЁЎеһӢи®ӯз»ғиҮіе…ійҮҚиҰҒгҖӮ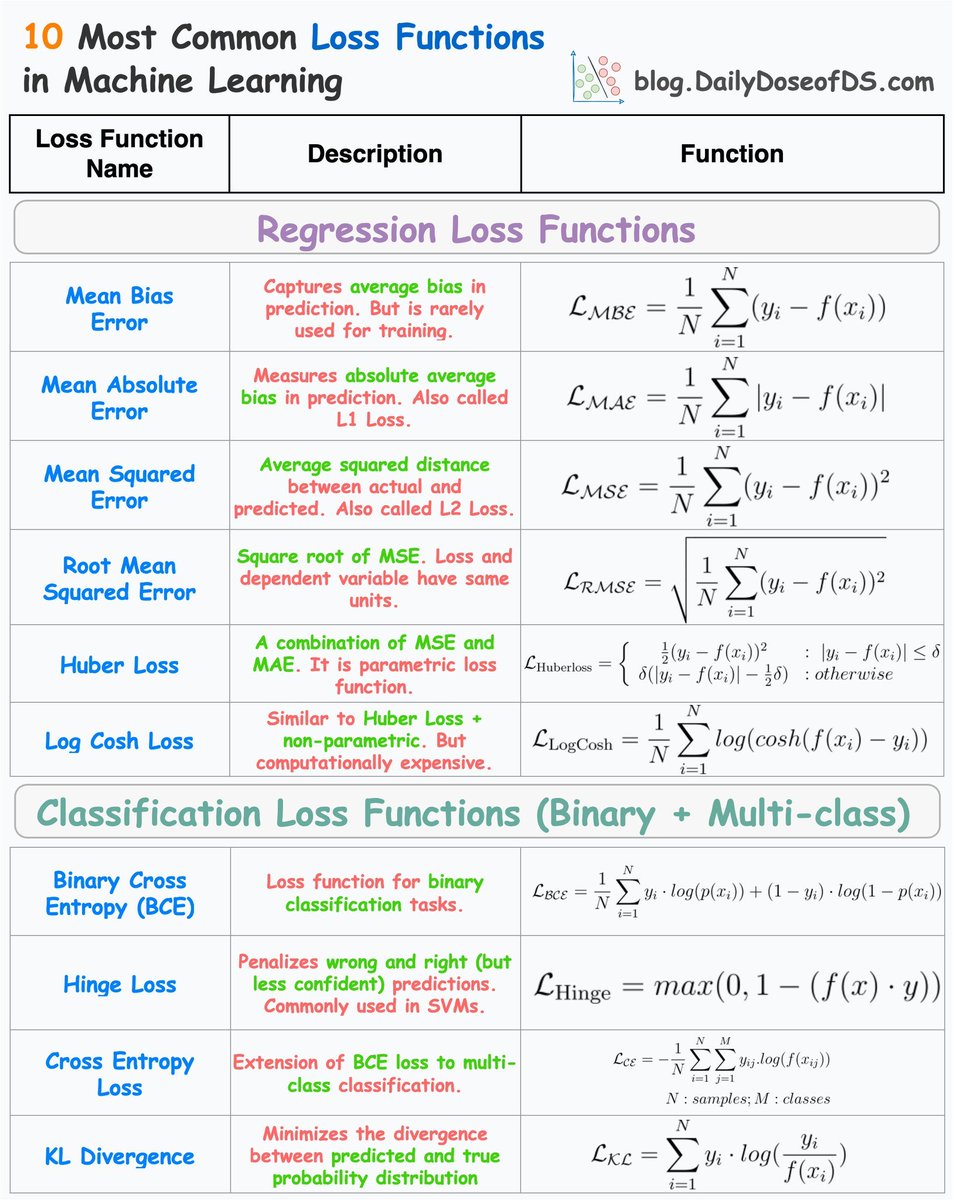
иҝҷеј еӣҫиЎЁеҲ—еҮәдәҶжңәеҷЁеӯҰд№ дёӯжңҖеёёз”Ёзҡ„10з§ҚжҚҹеӨұеҮҪж•°пјҢ并еҲҶдёәеӣһеҪ’е’ҢеҲҶзұ»дёӨзұ»пјҡ
еӣһеҪ’жҚҹеӨұеҮҪж•°
1. Mean Bias Error (MBE)
- жҸҸиҝ°пјҡжҚ•жҚүйў„жөӢдёӯзҡ„е№іеқҮеҒҸе·®пјҢдҪҶеҫҲе°‘з”ЁдәҺи®ӯз»ғгҖӮ
- е…¬ејҸпјҡ\[ L_{MBE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i)) \]
2. Mean Absolute Error (MAE)
- жҸҸиҝ°пјҡжөӢйҮҸйў„жөӢдёӯзҡ„з»қеҜ№е№іеқҮеҒҸе·®пјҢд№ҹз§°дёәL1жҚҹеӨұгҖӮ
- е…¬ејҸпјҡ\[ L_{MAE} = \frac{1}{N} \sum_{i=1}^{N} |y_i - f(x_i)| \]
3. Mean Squared Error (MSE)
- жҸҸиҝ°пјҡе®һйҷ…еҖјдёҺйў„жөӢеҖјд№Ӣй—ҙзҡ„е№іеқҮе№іж–№и·қзҰ»пјҢд№ҹз§°дёәL2жҚҹеӨұгҖӮ
- е…¬ејҸпјҡ\[ L_{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i))^2 \]
4. Root Mean Squared Error (RMSE)
- жҸҸиҝ°пјҡMSEзҡ„е№іж–№ж №пјҢжҚҹеӨұе’Ңеӣ еҸҳйҮҸе…·жңүзӣёеҗҢеҚ•дҪҚгҖӮ
- е…¬ејҸпјҡ\[ L_{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i - f(x_i))^2} \]
5. Huber Loss
- жҸҸиҝ°пјҡз»“еҗҲдәҶMSEе’ҢMAEпјҢжҳҜдёҖз§ҚеҸӮж•°еҢ–зҡ„жҚҹеӨұеҮҪж•°гҖӮ
- е…¬ејҸпјҡ
\[
L_{Huber\ loss} =
\begin{cases}
\frac{1}{2}(y_i-f(x_i))^2, & |y_i-f(x_i)| \leq \delta\\
\delta(|y_i-f(x_i)|-\frac{1}{2}\delta), & \text{otherwise}
\end{cases}
\]
6. Log Cosh Loss
- жҸҸиҝ°пјҡзұ»дјјдәҺHuber LossпјҢдҪҶйқһеҸӮж•°еҢ–пјҢи®Ўз®—дёҠиҫғжҳӮиҙөгҖӮ
- е…¬ејҸпјҡ\[ L_{Log\ Cosh} = \frac{1}{N} \sum_{i=1}^{N} log(cosh(f(x_i) - y_i)) \]
еҲҶзұ»жҚҹеӨұеҮҪж•°пјҲеҢ…еҗ«дәҢеҲҶзұ»е’ҢеӨҡеҲҶзұ»пјү
1. Binary Cross Entropy (BCE)
- жҸҸиҝ°пјҡз”ЁдәҺдәҢеҲҶзұ»д»»еҠЎзҡ„жҚҹеӨұеҮҪж•°гҖӮ
- е…¬ејҸпјҡ\[ L_{BCE} = -\frac{1}{N}\sum_{i=1}^{N}[y_i\cdot log(p(x_i)) + (1-y_i)\cdot log(1-p(x_i))] \]
2. Hinge Loss
- жҸҸиҝ°пјҡжғ©зҪҡй”ҷиҜҜе’ҢдёҚиҮӘдҝЎзҡ„йў„жөӢпјҢеёёз”ЁдәҺж”ҜжҢҒеҗ‘йҮҸжңәпјҲSVMпјүгҖӮ
- е…¬ејҸпјҡ\[ L_{Hinge} = max(0, 1-(f(x) \cdot y)) \]
3. Cross Entropy Loss
- жҸҸиҝ°пјҡBCEжҚҹеӨұеңЁеӨҡеҲҶзұ»дёҠзҡ„жү©еұ•гҖӮ
- е…¬ејҸпјҡ
\[
L_{CE} = -\frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{M}(y_{ij}\log(f(x_j)))
\]
пјҲе…¶дёӯ \( N: ж ·жң¬ж•°, M: зұ»еҲ«ж•° \)пјү
4. KL Divergence
- жҸҸиҝ°пјҡжңҖе°ҸеҢ–йў„жөӢжҰӮзҺҮдёҺзңҹе®һжҰӮзҺҮеҲҶеёғд№Ӣй—ҙзҡ„е·®ејӮгҖӮ
- е…¬ејҸпјҡ
\[
L_{KC} = N\sum y_i\cdot log(\frac{y_i}{f(x(i))})
\]
иҝҷдәӣжҚҹеӨұеҮҪж•°еңЁдёҚеҗҢд»»еҠЎдёӯеё®еҠ©дјҳеҢ–жЁЎеһӢжҖ§иғҪпјҢйҖүжӢ©еҗҲйҖӮзҡ„жҚҹеӨұеҮҪж•°еҜ№жЁЎеһӢи®ӯз»ғиҮіе…ійҮҚиҰҒгҖӮ

