Pruk on Nostr: ŗĻÉŗłôŗĻāŗł•ŗłĀŗłāŗł≠ŗłáŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆŗłôŗłĪŗĻČŗłô 1+1 ...
ŗĻÉŗłôŗĻāŗł•ŗłĀŗłāŗł≠ŗłáŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆŗłôŗłĪŗĻČŗłô 1+1 ŗĻĄŗł°ŗĻąŗĻÄŗłóŗĻąŗł≤ŗłĀŗłĪŗłö 2
ŗłĄŗłďŗłīŗłēŗł®ŗł≤ŗł™ŗłēŗł£ŗĻĆŗłóŗłĶŗĻąŗĻÄŗł£ŗł≤ŗĻÄŗł£ŗłĶŗłĘŗłôŗł°ŗł≤ŗłēŗłĪŗĻČŗłáŗĻĀŗłēŗĻąŗĻÄŗłĒŗĻáŗłĀŗłôŗłĪŗĻČŗłôŗĻÉŗłäŗĻČŗĻĄŗł°ŗĻąŗĻĄŗłĒŗĻČŗłĀŗłĪŗłöŗĻāŗł•ŗłĀŗłāŗł≠ŗłáŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆ
ŗĻÄŗłěŗł£ŗł≤ŗłįŗłôŗłīŗłĘŗł≤ŗł°ŗłĀŗł≤ŗł£ŗłöŗłßŗłĀŗĻĄŗł°ŗĻąŗĻÉŗłäŗĻąŗłĀŗł≤ŗł£ŗł£ŗłßŗł°ŗłĀŗłĪŗłôŗłāŗł≠ŗłáŗłēŗłĪŗłßŗĻÄŗł•ŗłā
ŗĻĀŗłēŗĻąŗłĄŗł∑ŗł≠ŗłĀŗł≤ŗł£ŗł•ŗł≤ŗłĀŗĻÄŗł™ŗĻČŗłôŗłēŗłĪŗłĒŗłúŗĻąŗł≤ŗłôŗłąŗłłŗłĒŗł™ŗł≠ŗłáŗłąŗłłŗłĒŗłöŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗĻĀŗł•ŗĻČŗłßŗłęŗł≤ŗł≠ŗłĶŗłĀŗłąŗłłŗłĒŗłóŗłĶŗĻąŗĻÄŗł™ŗĻČŗłôŗłēŗł£ŗłáŗłôŗłĪŗĻČŗłôŗłēŗłĪŗłĒŗłúŗĻąŗł≤ŗłô
ŗłčŗłĪŗłöŗłčŗĻČŗł≠ŗłôŗłāŗł∂ŗĻČŗłôŗł≠ŗłĶŗłĀŗłęŗłôŗĻąŗł≠ŗłĘŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗłóŗłĶŗĻąŗĻÉŗłäŗĻČŗĻÉŗłôŗłĀŗł≤ŗł£ŗĻÄŗłāŗĻČŗł≤ŗł£ŗłęŗłĪŗł™ŗĻÉŗłôŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆŗłĀŗĻáŗĻĄŗł°ŗĻąŗĻÉŗłäŗĻąŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗĻĀŗłöŗłöŗĻÉŗłôŗł£ŗłĻŗłõŗłčŗł∂ŗĻąŗłáŗł≠ŗłĘŗłĻŗĻąŗłöŗłôŗł£ŗłįŗłôŗł≤ŗłöŗłāŗł≠ŗłáŗłąŗł≥ŗłôŗłßŗłôŗłąŗł£ŗłīŗłá ŗĻĀŗłēŗĻąŗĻÄŗłõŗĻáŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗłöŗłôŗł£ŗłįŗłôŗł≤ŗłöŗłąŗł≥ŗłôŗłßŗłôŗĻÉŗłô Finite Field ŗłāŗł≠ŗłáŗłąŗł≥ŗłôŗłßŗłôŗĻÄŗłČŗłěŗł≤ŗłį 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1 ŗłčŗł∂ŗĻąŗłáŗłąŗłįŗĻĄŗłĒŗĻČŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗĻĀŗłöŗłöŗĻÉŗłęŗł°ŗĻąŗłóŗłĶŗĻąŗĻĄŗł°ŗĻąŗĻĄŗłĒŗĻČŗĻÄŗłęŗĻáŗłôŗĻĀŗłöŗłöŗĻÉŗłôŗł£ŗłĻŗłõŗłóŗłĪŗĻąŗłßŗĻĄŗłõ ŗłčŗł∂ŗĻąŗłáŗłĄŗłôŗłóŗłĪŗĻąŗłßŗĻĄŗłõŗłĒŗłĻŗĻĄŗł°ŗĻąŗł≠ŗł≠ŗłĀŗłęŗł£ŗł≠ŗłĀŗłßŗĻąŗł≤ŗł°ŗłĪŗłôŗĻÄŗłõŗĻáŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗłĘŗłĪŗłáŗĻĄŗłá

ŗłúŗł•ŗłóŗłĶŗĻąŗĻĄŗłĒŗĻČŗłĄŗł∑ŗł≠ŗłĀŗł≤ŗł£ŗłöŗłßŗłĀŗłēŗłĪŗłßŗĻÄŗł•ŗłāŗłóŗłĶŗĻąŗł™ŗłłŗłĒŗĻĀŗł™ŗłôŗłąŗłįŗłěŗłīŗł®ŗłĒŗł≤ŗł£ ŗĻĀŗł•ŗłįŗĻÄŗł°ŗł∑ŗĻąŗł≠ŗłĀŗł≤ŗł£ŗłöŗłßŗłĀŗĻÄŗłĀŗłīŗłĒŗłāŗł∂ŗĻČŗłôŗłčŗĻČŗł≥ŗłĀŗłĪŗłôŗłąŗł∂ŗłáŗĻÄŗłĀŗłīŗłĒŗĻÄŗłõŗĻáŗłôŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗł£ŗłĻŗłõŗĻĀŗłöŗłöŗĻÉŗłęŗł°ŗĻąŗłāŗł∂ŗĻČŗłôŗłóŗłĶŗĻąŗĻĄŗł°ŗĻąŗł™ŗł≤ŗł°ŗł≤ŗł£ŗłłŗłĄŗł≥ŗłôŗłßŗłďŗłęŗł≤ŗłĀŗł≤ŗł£ŗłĘŗĻČŗł≠ŗłôŗłĀŗł•ŗłĪŗłöŗĻĄŗłĒŗĻČ
ŗłĒŗĻČŗłßŗłĘŗłĄŗłßŗł≤ŗł°ŗłĄŗłłŗłďŗł™ŗł°ŗłöŗłĪŗłēŗłīŗłāŗł≠ŗłáŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗłóŗłĶŗĻąŗĻĄŗł°ŗĻąŗłĘŗĻČŗł≠ŗłôŗłĀŗł•ŗłĪŗłöŗĻĄŗłĒŗĻČŗłôŗłĶŗĻąŗĻĀŗłęŗł•ŗłįŗłąŗł∂ŗłáŗłĖŗłĻŗłĀŗłôŗł≥ŗł°ŗł≤ŗĻÉŗłäŗĻČŗĻÉŗłôŗłĀŗł≤ŗł£ŗłĄŗł≥ŗłôŗłßŗłďŗłęŗł≤ public key (P) ŗłąŗł≤ŗłĀ private key (p)
P =pG ŗĻÄŗł°ŗł∑ŗĻąŗł≠ G ŗłĄŗł∑ŗł≠ŗłĄŗĻąŗł≤ŗłĄŗłáŗłóŗłĶŗĻąŗłöŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀ
ŗłĖŗł∂ŗłáŗĻĀŗł°ŗĻČŗłßŗĻąŗł≤ŗł™ŗł°ŗłĀŗł≤ŗł£ŗłĒŗłĪŗłáŗłĀŗł•ŗĻąŗł≤ŗłßŗłąŗłįŗłĒŗłĻŗĻÄŗłęŗł°ŗł∑ŗł≠ŗłôŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗłáŗĻąŗł≤ŗłĘ ŗĻÜ ŗĻĀŗłēŗĻąŗĻāŗłĄŗłēŗł£ŗłčŗłĪŗłöŗłčŗĻČŗł≠ŗłôŗĻĀŗł•ŗłįŗłěŗłīŗł™ŗłĒŗł≤ŗł£ŗĻÄŗłěŗł£ŗł≤ŗłįŗł°ŗłĪŗłôŗłĄŗł∑ŗł≠ŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗłöŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗĻÉŗłôŗł£ŗłįŗłôŗł≤ŗłöŗłąŗł≥ŗłôŗłßŗłôŗĻÉŗłô Finite Field ŗłāŗł≠ŗłáŗłąŗł≥ŗłôŗłßŗłôŗĻÄŗłČŗłěŗł≤ŗłį 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 ŗłóŗłĶŗĻąŗĻÄŗłõŗĻáŗłôŗĻÄŗł£ŗł∑ŗĻąŗł≠ŗłáŗłĘŗł≤ŗłĀŗł°ŗł≤ŗłĀŗłóŗłĶŗĻąŗłąŗłįŗłęŗł≤ŗłĀŗł≤ŗł£ŗłĒŗł≥ŗĻÄŗłôŗłīŗłôŗłĀŗł≤ŗł£ŗłóŗłĶŗĻąŗłĘŗĻČŗł≠ŗłôŗłĀŗł•ŗłĪŗłöŗĻĄŗłĒŗĻČ
ŗłóŗłĪŗĻČŗłáŗłęŗł°ŗłĒŗłôŗłĶŗĻČŗłĀŗĻáŗłĄŗł∑ŗł≠ŗłóŗłĶŗĻąŗł°ŗł≤ŗĻĀŗłöŗłöŗłĄŗł£ŗĻąŗł≤ŗłß ŗĻÜ ŗłāŗł≠ŗłá asymmetric encryption ŗłóŗłĶŗĻąŗłĖŗłĻŗłĀŗłôŗł≥ŗł°ŗł≤ŗłõŗł£ŗłįŗłĘŗłłŗłĀŗłēŗĻĆŗĻÉŗłäŗĻČŗĻÉŗłôŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆ
#siamstr
ŗłĄŗłďŗłīŗłēŗł®ŗł≤ŗł™ŗłēŗł£ŗĻĆŗłóŗłĶŗĻąŗĻÄŗł£ŗł≤ŗĻÄŗł£ŗłĶŗłĘŗłôŗł°ŗł≤ŗłēŗłĪŗĻČŗłáŗĻĀŗłēŗĻąŗĻÄŗłĒŗĻáŗłĀŗłôŗłĪŗĻČŗłôŗĻÉŗłäŗĻČŗĻĄŗł°ŗĻąŗĻĄŗłĒŗĻČŗłĀŗłĪŗłöŗĻāŗł•ŗłĀŗłāŗł≠ŗłáŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆ
ŗĻÄŗłěŗł£ŗł≤ŗłįŗłôŗłīŗłĘŗł≤ŗł°ŗłĀŗł≤ŗł£ŗłöŗłßŗłĀŗĻĄŗł°ŗĻąŗĻÉŗłäŗĻąŗłĀŗł≤ŗł£ŗł£ŗłßŗł°ŗłĀŗłĪŗłôŗłāŗł≠ŗłáŗłēŗłĪŗłßŗĻÄŗł•ŗłā
ŗĻĀŗłēŗĻąŗłĄŗł∑ŗł≠ŗłĀŗł≤ŗł£ŗł•ŗł≤ŗłĀŗĻÄŗł™ŗĻČŗłôŗłēŗłĪŗłĒŗłúŗĻąŗł≤ŗłôŗłąŗłłŗłĒŗł™ŗł≠ŗłáŗłąŗłłŗłĒŗłöŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗĻĀŗł•ŗĻČŗłßŗłęŗł≤ŗł≠ŗłĶŗłĀŗłąŗłłŗłĒŗłóŗłĶŗĻąŗĻÄŗł™ŗĻČŗłôŗłēŗł£ŗłáŗłôŗłĪŗĻČŗłôŗłēŗłĪŗłĒŗłúŗĻąŗł≤ŗłô
ŗłčŗłĪŗłöŗłčŗĻČŗł≠ŗłôŗłāŗł∂ŗĻČŗłôŗł≠ŗłĶŗłĀŗłęŗłôŗĻąŗł≠ŗłĘŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗłóŗłĶŗĻąŗĻÉŗłäŗĻČŗĻÉŗłôŗłĀŗł≤ŗł£ŗĻÄŗłāŗĻČŗł≤ŗł£ŗłęŗłĪŗł™ŗĻÉŗłôŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆŗłĀŗĻáŗĻĄŗł°ŗĻąŗĻÉŗłäŗĻąŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗĻĀŗłöŗłöŗĻÉŗłôŗł£ŗłĻŗłõŗłčŗł∂ŗĻąŗłáŗł≠ŗłĘŗłĻŗĻąŗłöŗłôŗł£ŗłįŗłôŗł≤ŗłöŗłāŗł≠ŗłáŗłąŗł≥ŗłôŗłßŗłôŗłąŗł£ŗłīŗłá ŗĻĀŗłēŗĻąŗĻÄŗłõŗĻáŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗłöŗłôŗł£ŗłįŗłôŗł≤ŗłöŗłąŗł≥ŗłôŗłßŗłôŗĻÉŗłô Finite Field ŗłāŗł≠ŗłáŗłąŗł≥ŗłôŗłßŗłôŗĻÄŗłČŗłěŗł≤ŗłį 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1 ŗłčŗł∂ŗĻąŗłáŗłąŗłįŗĻĄŗłĒŗĻČŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗĻĀŗłöŗłöŗĻÉŗłęŗł°ŗĻąŗłóŗłĶŗĻąŗĻĄŗł°ŗĻąŗĻĄŗłĒŗĻČŗĻÄŗłęŗĻáŗłôŗĻĀŗłöŗłöŗĻÉŗłôŗł£ŗłĻŗłõŗłóŗłĪŗĻąŗłßŗĻĄŗłõ ŗłčŗł∂ŗĻąŗłáŗłĄŗłôŗłóŗłĪŗĻąŗłßŗĻĄŗłõŗłĒŗłĻŗĻĄŗł°ŗĻąŗł≠ŗł≠ŗłĀŗłęŗł£ŗł≠ŗłĀŗłßŗĻąŗł≤ŗł°ŗłĪŗłôŗĻÄŗłõŗĻáŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗłĘŗłĪŗłáŗĻĄŗłá

ŗłúŗł•ŗłóŗłĶŗĻąŗĻĄŗłĒŗĻČŗłĄŗł∑ŗł≠ŗłĀŗł≤ŗł£ŗłöŗłßŗłĀŗłēŗłĪŗłßŗĻÄŗł•ŗłāŗłóŗłĶŗĻąŗł™ŗłłŗłĒŗĻĀŗł™ŗłôŗłąŗłįŗłěŗłīŗł®ŗłĒŗł≤ŗł£ ŗĻĀŗł•ŗłįŗĻÄŗł°ŗł∑ŗĻąŗł≠ŗłĀŗł≤ŗł£ŗłöŗłßŗłĀŗĻÄŗłĀŗłīŗłĒŗłāŗł∂ŗĻČŗłôŗłčŗĻČŗł≥ŗłĀŗłĪŗłôŗłąŗł∂ŗłáŗĻÄŗłĀŗłīŗłĒŗĻÄŗłõŗĻáŗłôŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗł£ŗłĻŗłõŗĻĀŗłöŗłöŗĻÉŗłęŗł°ŗĻąŗłāŗł∂ŗĻČŗłôŗłóŗłĶŗĻąŗĻĄŗł°ŗĻąŗł™ŗł≤ŗł°ŗł≤ŗł£ŗłłŗłĄŗł≥ŗłôŗłßŗłďŗłęŗł≤ŗłĀŗł≤ŗł£ŗłĘŗĻČŗł≠ŗłôŗłĀŗł•ŗłĪŗłöŗĻĄŗłĒŗĻČ
ŗłĒŗĻČŗłßŗłĘŗłĄŗłßŗł≤ŗł°ŗłĄŗłłŗłďŗł™ŗł°ŗłöŗłĪŗłēŗłīŗłāŗł≠ŗłáŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗłóŗłĶŗĻąŗĻĄŗł°ŗĻąŗłĘŗĻČŗł≠ŗłôŗłĀŗł•ŗłĪŗłöŗĻĄŗłĒŗĻČŗłôŗłĶŗĻąŗĻĀŗłęŗł•ŗłįŗłąŗł∂ŗłáŗłĖŗłĻŗłĀŗłôŗł≥ŗł°ŗł≤ŗĻÉŗłäŗĻČŗĻÉŗłôŗłĀŗł≤ŗł£ŗłĄŗł≥ŗłôŗłßŗłďŗłęŗł≤ public key (P) ŗłąŗł≤ŗłĀ private key (p)
P =pG ŗĻÄŗł°ŗł∑ŗĻąŗł≠ G ŗłĄŗł∑ŗł≠ŗłĄŗĻąŗł≤ŗłĄŗłáŗłóŗłĶŗĻąŗłöŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀ
ŗłĖŗł∂ŗłáŗĻĀŗł°ŗĻČŗłßŗĻąŗł≤ŗł™ŗł°ŗłĀŗł≤ŗł£ŗłĒŗłĪŗłáŗłĀŗł•ŗĻąŗł≤ŗłßŗłąŗłįŗłĒŗłĻŗĻÄŗłęŗł°ŗł∑ŗł≠ŗłôŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗłáŗĻąŗł≤ŗłĘ ŗĻÜ ŗĻĀŗłēŗĻąŗĻāŗłĄŗłēŗł£ŗłčŗłĪŗłöŗłčŗĻČŗł≠ŗłôŗĻĀŗł•ŗłįŗłěŗłīŗł™ŗłĒŗł≤ŗł£ŗĻÄŗłěŗł£ŗł≤ŗłįŗł°ŗłĪŗłôŗłĄŗł∑ŗł≠ŗłĀŗł≤ŗł£ŗłĄŗłĻŗłďŗłöŗłôŗĻÄŗł™ŗĻČŗłôŗĻāŗłĄŗĻČŗłáŗł≠ŗłīŗł•ŗł•ŗłīŗłõŗłēŗłīŗłĀŗĻÉŗłôŗł£ŗłįŗłôŗł≤ŗłöŗłąŗł≥ŗłôŗłßŗłôŗĻÉŗłô Finite Field ŗłāŗł≠ŗłáŗłąŗł≥ŗłôŗłßŗłôŗĻÄŗłČŗłěŗł≤ŗłį 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 ŗłóŗłĶŗĻąŗĻÄŗłõŗĻáŗłôŗĻÄŗł£ŗł∑ŗĻąŗł≠ŗłáŗłĘŗł≤ŗłĀŗł°ŗł≤ŗłĀŗłóŗłĶŗĻąŗłąŗłįŗłęŗł≤ŗłĀŗł≤ŗł£ŗłĒŗł≥ŗĻÄŗłôŗłīŗłôŗłĀŗł≤ŗł£ŗłóŗłĶŗĻąŗłĘŗĻČŗł≠ŗłôŗłĀŗł•ŗłĪŗłöŗĻĄŗłĒŗĻČ
ŗłóŗłĪŗĻČŗłáŗłęŗł°ŗłĒŗłôŗłĶŗĻČŗłĀŗĻáŗłĄŗł∑ŗł≠ŗłóŗłĶŗĻąŗł°ŗł≤ŗĻĀŗłöŗłöŗłĄŗł£ŗĻąŗł≤ŗłß ŗĻÜ ŗłāŗł≠ŗłá asymmetric encryption ŗłóŗłĶŗĻąŗłĖŗłĻŗłĀŗłôŗł≥ŗł°ŗł≤ŗłõŗł£ŗłįŗłĘŗłłŗłĀŗłēŗĻĆŗĻÉŗłäŗĻČŗĻÉŗłôŗłöŗłīŗłēŗłĄŗł≠ŗłĘŗłôŗĻĆ
#siamstr
quoting nevent1q‚Ķlu4jŤ≤ĚťćěŚćŹŤģģ¬∑ Śüļšļ霧≠ŚúÜśõ≤ÁļŅťÖćÁāĻ
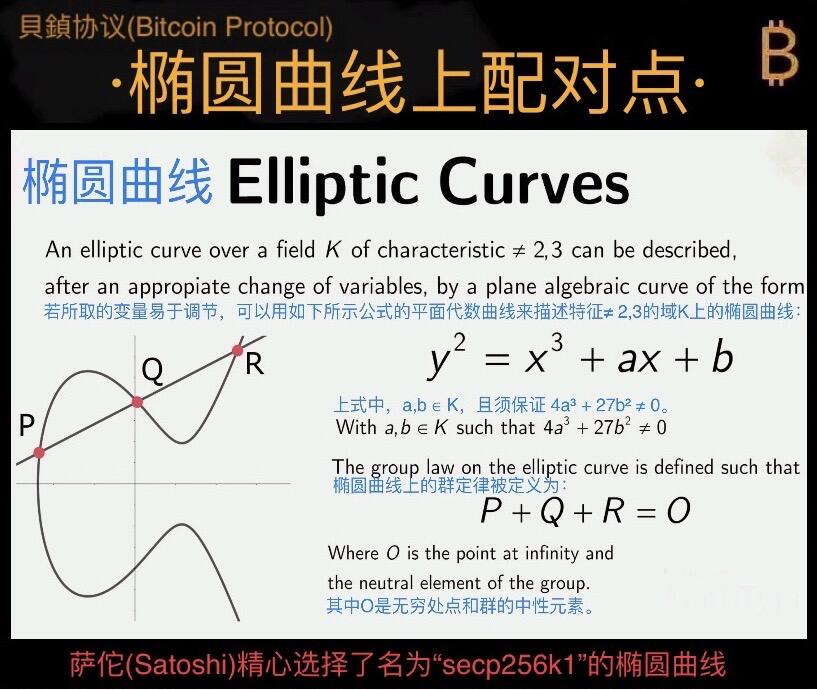
Bitcoin Protocol · Encryption and decryption based on elliptic curve
#Ť≤Ěťćě(#Bitcoin ) #ś§≠ŚúÜśõ≤ÁļŅ(#Elliptic_curve) #Ťź®šĹó(#Satoshi)